Bangun Datar

Bangun datar merupakan salah satu materi dasar yang dipelajari dalam matematika. Pada kesempatan kali ini kita akan bahas secara lengkap mengenai bangun datar.

Pengertian Bangun Datar

Bangun datar merupakan suatu bidang datar yang dibatasi oleh garis-garis lurus atau garis lengkung.

Atau lebih tepatnya suatu bangun yang memiliki bidang rata serta mempunyai dua dimensi. Yakni panjang dan lebar namun tidak mempunyai tinggi atau ketebalan.

Dengan begitu, pengertian singkatnya dari bangun datar adalah abstrak.

Jenis Bangun Datar

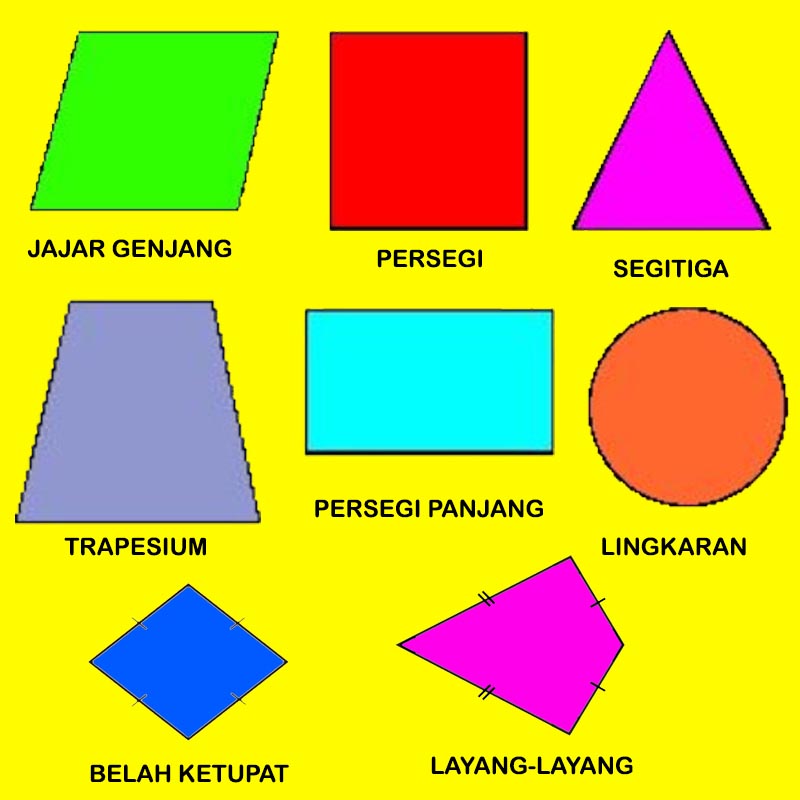
Dalam matematika, ada 8 jenis bangun datar yang dapat dipelajari yaitu:

1. Persegi,
2. Persegi Panjang,
3. Segitiga,
4. Jajar Genjang,
5. Trapesium,
6. Belah Ketupat,
7. Layang-layang, dan
8. Lingkaran.

Rumus Bangun Datar

Berikut ini akan kami jelaskan macam atau jenis dari bangun datar beserta sifatnya. Perhatikan ulasan berikut ini.

1. Persegi

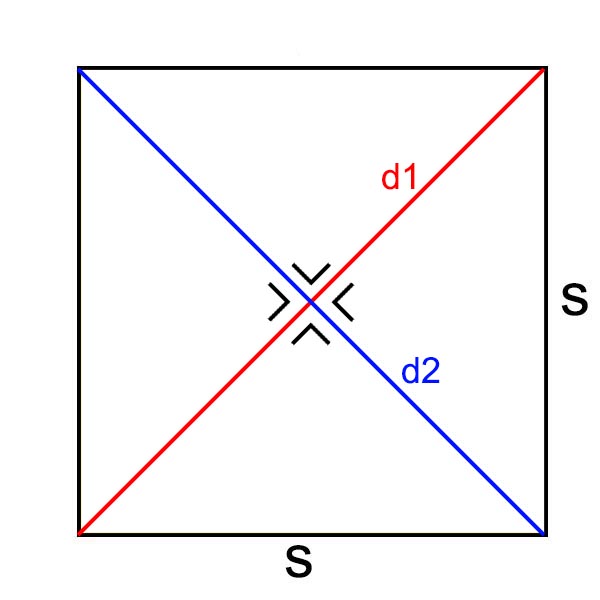
Persegi adalah suatu bangun datar 2 dimensi yang dibentuk oleh 4 buah rusuk yang memiliki ukuran sama panjang. Dan juga memiliki 4 buah sudut siku – siku.

Sehingga kita dapat menyimpulkan bahwa persegi memiliki sisi-sisi yang sama panjang, dan sudut-sudut yang sama besar.

Sifat-sifat Persegi

• Semua sisinya memiliki ukuran panjang yang sama dan juga sisinya berhadapan sejajar.
• Semua sudutnya adalah sudut siku-siku atau 90º.
• Memiliki dua diagonal yang sama panjang, berpotongan tepat di tengah-tengah dan membentuk sudut siku-siku.
• Diagonal persegi membagi dua masing-masing sudutnya.
• Memiliki empat sumbu simetri.

Rumus-Rumus Persegi

Berikut ini adalah beberapa rumus yang biasa digunakan pada bangun persegi, antara lain:

Nama	Rumus
Luas Persegi	L = s × s
	L = (K/4)²
	L = ½ × d²
Keliling	K = 4s
Diagonal	d = s × √2
Sisi	s = √L
	s = K÷4
	s = d÷√2

Keterangan:

• L = Luas
• K = Keliling
• s = Sisi
• d = diagonal

Contoh Soal:

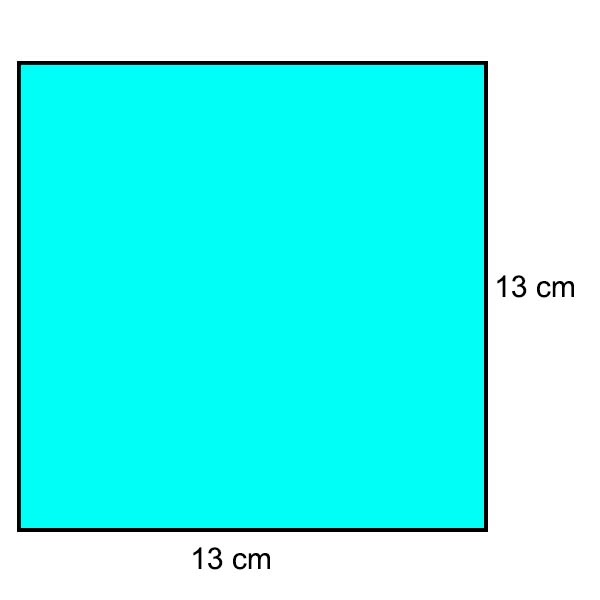
Jika suatu persegi memiliki panjang sisi 13 cm, berapakah luas dan keliling persegi tersebut?

Penyelesaian :

Diketahui s = 13 cm

L = s × s
L = 13 × 13
L = 169 cm²

K = 4s
K = 4×13
K = 52 cm

Jadi, luas persegi tersebut adalah 169 cm² dan kelilingnya adalah 52 cm.

2. Persegi Panjang

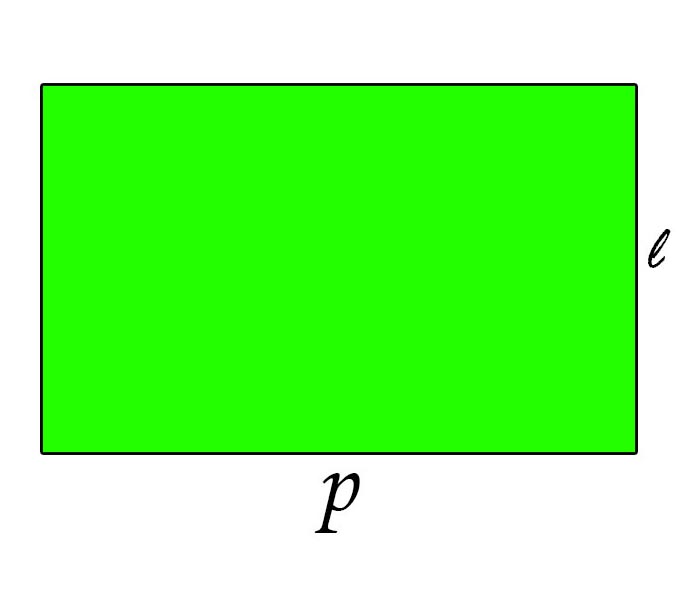
Persegi panjang meurpakan suatu bangun datar 2 dimensi yang dibentuk oleh 2 buah pasang rusuk yang panjang serta sejajar dan juga memiliki 4 sudut siku–siku.

Sifat-sifat persegi panjang

• Sisi-sisi yang berhadapan memiliki ukuran yang sama panjang dan juga sejajar.
• Semua sudutnya merupakan sudut siku-siku.
• Mempunyai dua diagonal yang sama panjang dan saling berpotongan di titik pusat bangun persegi panjang. Titik tersebut adalah membagi dua diagonal dengan ukuran sama panjang.
• Mempunyai dua buah sumbu simetri yaitu sumbu vertikal dan juga sumbu horizontal.

Rumus-Rumus Persegi Panjang

Nama	Rumus
Luas	L = p × l
Keliling	K = 2 (p + l)
Diagonal	d = √(p² + l²)
Panjang	p = L ÷ l
	p = K ÷ 2 – l
	p = √ (d² – l²)
Lebar	l = L ÷ p
	l = K ÷ 2 – p
	l = √(d² – p²)

Keterangan:

• L = Luas
• K = Keliling
• p = Panjang
• l = Lebar
• d = Diagonal

Contoh Soal

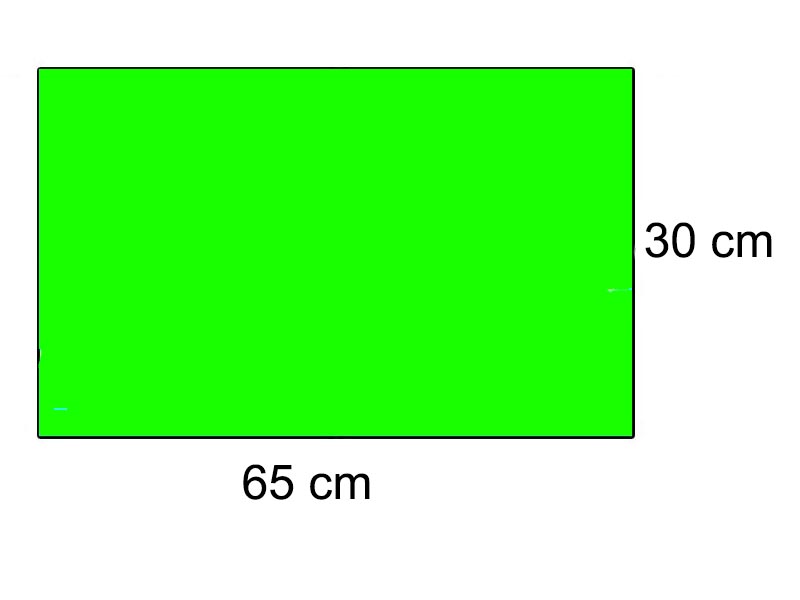
Hitunglah keliling dan luas persegi panjang yang memiliki panjang sisi 65 cm dan 30 cm!

Penyelesaian

Diketahui p = 65 cm dan l = 30 cm

K = 2(p+l)
K = 2 (65+30)
K = 2 × 95
K = 190 cm

L = p×l
L = 65×30
L = 1950 cm²

Jadi, keliling persegi panjang tersebut adalah 190 cm dan luasnya adalah 1950 cm².

Biar makin paham dengan rumus keliling persegi, silahkan simak video berikut ini.

3. Segitiga

Segitiga merupakan suatu bangun datar 2 dimensi yang dibentuk oleh 3 buah sisi yang berupa garis lurus serta memiliki 3 buah sudut.

Sehingga bangun datar yang terbentuk dari tiga garis lurus disebut sebagai segitiga.

Sifat-Sifat Segitiga

• Pada bangun segitiga, ketiga sudutnya jika dijumlahkan memiliki besar 180º.
• Sifat Segitiga mempunyai 3 sisi serta 3 titik sudut.

Rumus-Rumus Segitiga

Nama	Rumus
Luas	L = ½ × a × t
	L = √(s × (s-a) × (s-b)× (s-c))
Keliling	K = a+b+c
	K = Jumlah Semua Sisi
Alas	a = 2L ÷ t
Tinggi (t)	t = 2L ÷ a

Keterangan :

• L = Luas
• K = Keliling
• s = ½ Keliling
• a = alas segitiga
• t = tinggi segitiga
• b = sisi segitiga
• c = sisi segitiga

Contoh Soal

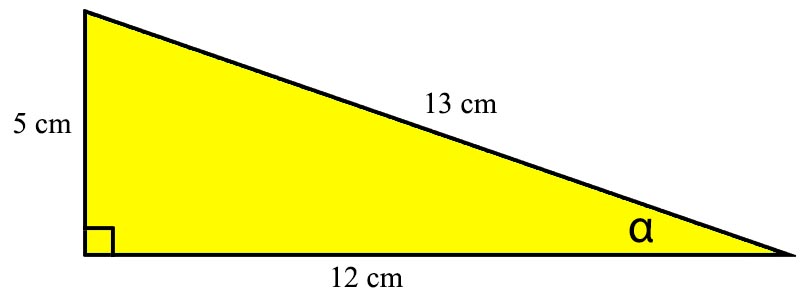
Hitunglah luas dan keliling segitiga siku-siku di atas!

Penyelesaian

Diketahui a = 12 cm, b atau t = 5 cm, dan c = 13 cm

L = ½ × a × t
L = ½ × 12 × 5
L = 6 × 5
L = 30 cm²

K = a + b + c
K = 12 + 5 + 13
K = 30 cm

Jadi, luas segitiga tersebut adalah 30 cm² dan kelilingnya adalah 30 cm.

4. Jajar genjang

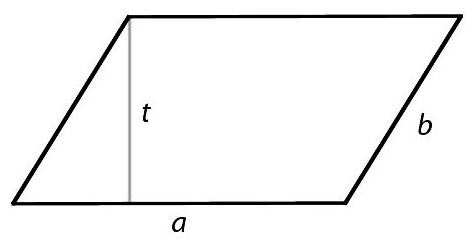
Pengertian dari jajar genjang sendiri merupakan suatu bangun datar 2 dimensi yang dibentuk atas 2 buah pasang rusuk yang sama panjang.

Serta memiliki dua pasang sudut yang sama besar, yakni sudut lancip dan sudut tumpul.

Sifat-Sifat Jajar genjang

• Tidak memiliki simetri lipat.
• Memiliki simetri putar tingkat dua.
• Sudut-sudut yang berhadapan memiliki ukuran yang sama besar.
• Memiliki 4 sisi serta 4 sisi sudut.
• Diagonal jajar genjang tidak sama panjang.
• Memiliki 2 Pasang Sisi yang sejajar serta sama panjang.
• Memiliki 2 buah sudut tumpul dan 2 buah sudut lancip.

Rumus-Rumus Jajar genjang

Nama	Rumus
Luas	L = a × t
Keliling	K = 2 (a + b)
Sisi Alas	a = (K/2) – b
	a = L/t
Tinggi	t = L/a
Sisi Miring	b = (K/2) – a

Keterangan

• L = Luas
• K = Keliling
• a = sisi alas
• t = tinggi
• b = sisi miring

Contoh Soal

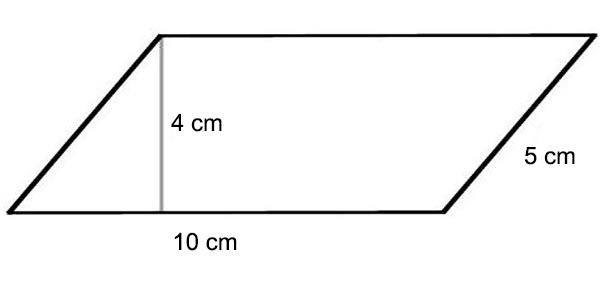
Berapakah luas dan keliling jajar genjang di tersebut?

Penyelesaian

Diketahui a = 10 cm, b = 5 cm, dan t = 4 cm

L = a × t
L = 10 × 4
L = 40 cm²

K = 2(a+b)
K = 2(10+5)
K = 2×15
K = 30 cm

Jadi luas jajar genjang di atas adalah 40 cm² dan kelilingnya adalah 30 cm.

Biar makin paham dengan rumus keliling jajar genjang, silahkan simak video berikut ini.

5. Trapesium

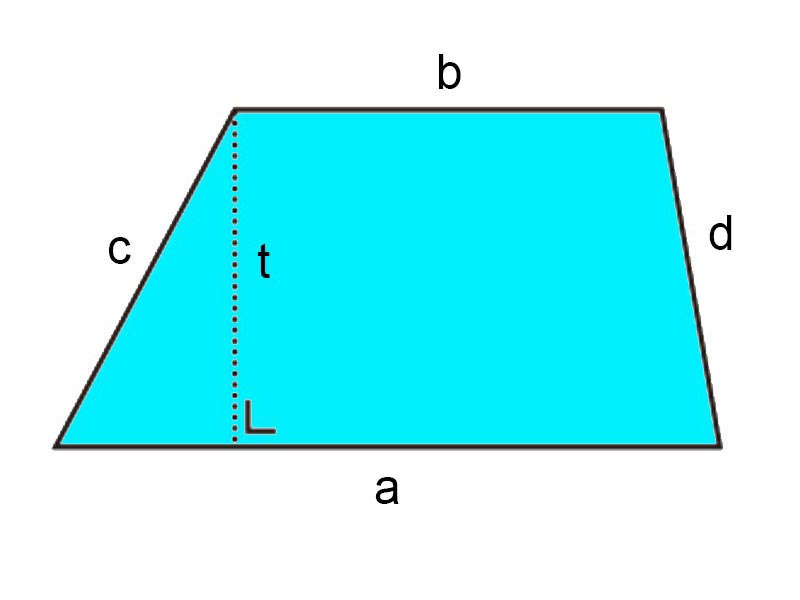
Trapesium sendiri merupakan suatu bangun datar 2 dimensi yang dibentuk dari 4 buah rusuk. 2 rusuk di antaranya saling sejajar namun panjang nya tidak sama.

Namun ada juga trapesium yang rusuk ketiganya membentuk sudut tegak lurus pada rusuk – rusuk sejajar. Trapesium yang memiliki sisi tegak biasa dikenal dengan sebutan trapesium siku – siku.

Sifat-sifat Trapesium

• Trapesium termasuk bangun datar yang terdiri dari 4 sisi (quadrilateral).
• Memiliki 2 sisi sejajar namun tidak sama panjang.
• Memiliki 4 titik sudut.
• Pada bagun datar trapesium setidaknya memiliki 1 titik sudut tumpul.
• Memiliki 1 simetri putar.

Rumus-Rumus Trapesium

Nama	Rumus
Luas	L = ½ × (a+b) × t
Keliling	K = a + b + c + d
Tinggi	t = 2L / (a+b)
Sisi a	a = 2L / t – b
	a = K – b – c – d
Sisi b	b = 2L / t – a
	b = K – a – c – d
Sisi c	c = K – a -b – d
Sisi d	d = K – a – b – c

Keterangan

• L = Luas
• K = Keliling
• t = tinggi
• a = sisi a
• b = sisi b
• c = sisi c
• d = sisi d

Contoh soal

Hitunglah keliling dan luas trapesium berikut ini!

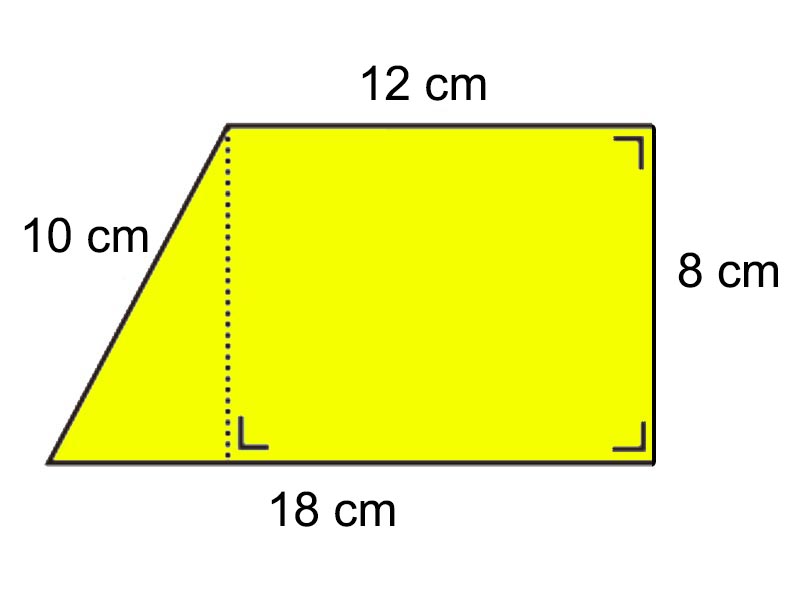
Penyelesaian

Diketahui a = 18 cm, b = 12 cm, c = 10 cm, t atau d = 8 cm

K = a + b + c + d
K = 18 + 12 +10 + 8
K = 30 + 18
K = 48 cm

L = ½ × (a+b) × t
L = ½ × (18+12) × 8
L = ½ × (30) × 8
L = 15 × 8
L = 120 cm²

Jadi, keliling trapesium tersebut adalah 48 cm dan luasnya adalah 120 cm².

Biar makin paham dengan rumus keliling trapesium. Silahkan simak video pembelajaran berikut ini.

6. Layang – layang

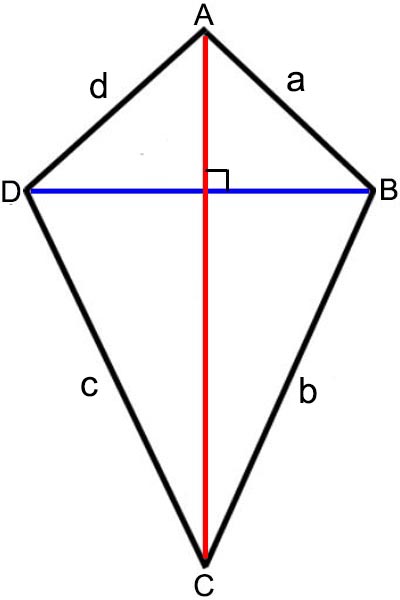
Layang-layang merupakan suatu bangun datar 2 dimensi yang di bentuk oleh 2 pasang sisi yang sama panjang, yang diagonalnya berpotongan dan saling tegak lurus.

Atau jika dilihat dari sudut pandang lain, layang-layang merupakan bangun datar yang dibentuk oleh dua segitiga sama kaki yang alasnya saling berimpit.

Sifat Layang–layang

• Layang-layang termasuk bangun datar dengan 4 sisi (quadrilateral).
• Memiliki 2 pasangan sisi yang sama panjang dan membentuk sudut yang berbeda.
  Pasangan 1 merupakan sisi a dan b, membentuk sudut ∠ABC.
  Pasangan 2 merupakan sisi c dan d, membentuk sudut ∠ADC.
• Memiliki sepasang sudut yang saling berhadapan yang sama besar.
  Sudut ∠BAD serta ∠BCD saling berhadapan dan memiliki besar yang sama.
• Memiliki 2 diagonal dengan yang panjang nya berbeda.
• Diagonal layang-layang saling tegak lurus (90º).
• Diagonal terpanjang merupakan sumbu simetri layang-layang.
• Layang-layang hanya mempunyai 1 sumbu simetri.

Rumus Layang–layang

Nama	Rumus
Luas	L = ½ × d1 × d2
Diagonal 1	d1 = 2L / d2
Diagonal 2	d2 = 2L / d1
Keliling	K = 2 × (a+b)
Sisi Pendek	a = K/2 – b
Sisi Panjang	b = K/2 – a

Keterangan

• L = Luas
• K = Keliling
• d1 = Diagonal 1
• d2 = Diagonal 2
• a = sisi pendek
• b = sisi panjang

Contoh Soal

Hitunglah luas layang layang yang memiliki panjang diagonal 6 cm dan 10 cm!

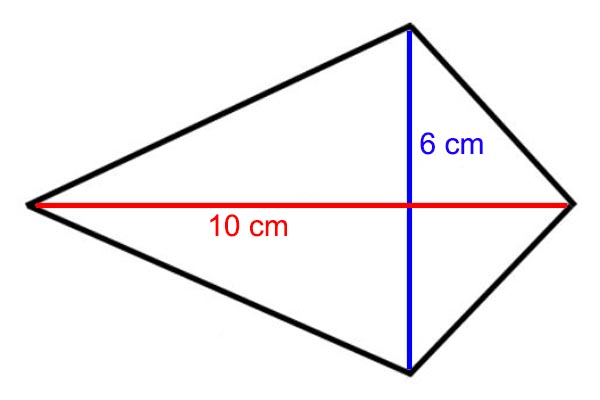
Penyelesaian

Diketahui d1 = 6 cm dan d2 = 10 cm

L = ½ × d1 × d2

L = ½ × 6 × 10

L = 3 × 10

L = 30 cm²

Jadi, luas layang-layang tersebut adalah 30 cm².

7. Belah Ketupat

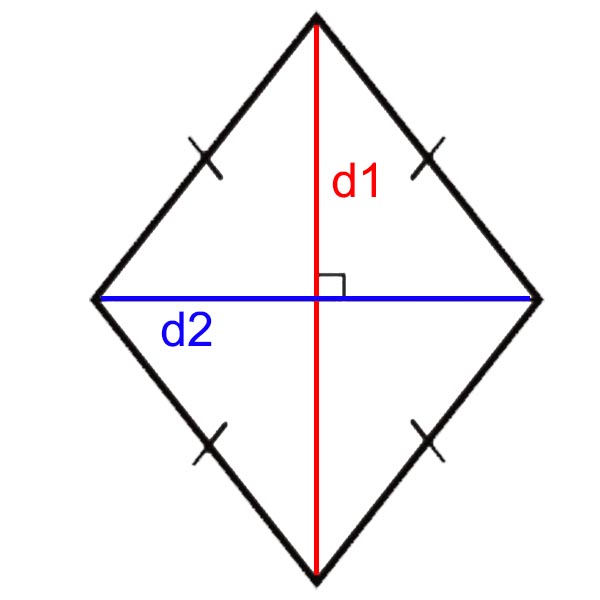
Belah Ketupat adalah bangun datar 2 dimensi yang dibentuk oleh 4 buah sisi yang sama panjang.

Serta memiliki 2 pasang sudut yang sama besar. Dalam bahasa inggris, belah ketupat disebut sebagai rhombus.

Sifat Belah Ketupat

• Keempat sisinya sama panjang.
• Memiliki 2 diagonal yang saling tegak lurus.
• Diagonal 1 (d1) dan diagonal 2 (d2) pada belah ketupat saling tegak lurus membentuk sudut siku-siku (90°).
• Sudut yang saling berhadapan sama besar.
  Pada belah ketupat sudut yang berhadapan memiliki besar yang sama.
• Jumlah keempat sudutnya 360º.
• Memiliki 2 sumbu simetri yaitu tepat pada diagonalnya.
• Memiliki Simetri Putar tingkat 2.
• Memiliki 4 buah sisi dan 4 titik sudut.

Rumus Belah Ketupat

Nama	Rumus
Luas	L = ½ × d1 × d2
Diagonal 1	d1 = 2L / d2
Diagonal 2	d2 = 2L / d1
Keliling	K = 4s
Sisi	s = K/4
	s = √((½d1)² + (½d2)²)

Keterangan

• L = Luas
• K = Keliling
• d1 = Diagonal 1
• d2 = Diagonal 2
• s = sisi

Contoh Soal

Berapakah keliling dan luas belah ketupat yang memiliki panjang diagonal 6 cm dan 8 cm serta panjang sisinya 5 cm?

Penyelesaian

Diketahui d1 = 6 cm, d2 = 8 cm, dan s = 5 cm

L = ½ × d1 × d2

L = ½ × 6 × 8

L = 3 × 8

L = 24 cm²

K = 4s

K = 4 × 5

K = 20 cm

Jadi, luas belah ketupat tersebut adalah 24 cm² dan kelilingnya adalah 20 cm.

Biar makin paham dengan rumus keliling belah ketupat, silahkan simak video berikut ini.

8. Lingkaran

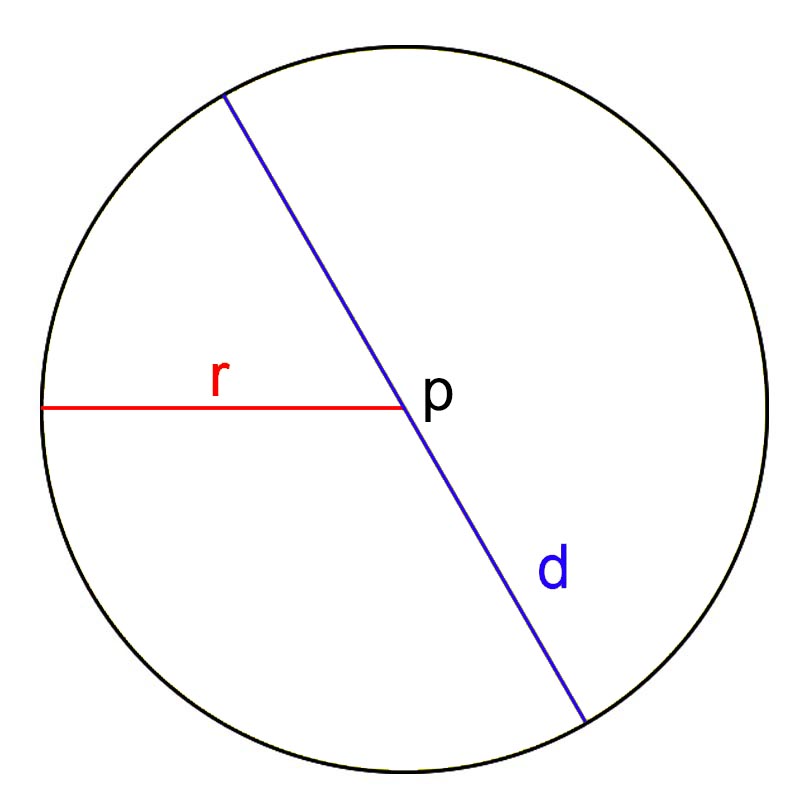
Lingkaran adalah bangun datar dua dimensi terbentuk bentuk oleh himpunan semua titik yang mempunyai jarak sama dari suatu titik tetap (pusat lingkaran).

• Pusat lingkaran (P): Titik tetap yang berada tepat di tengah-tengah lingkaran disebut sebagai pusat lingkaran.
• Jari-jari (r): jarak antara titik pusat lingkaran dengan titik yang lain disebut sebagai jari-jari lingkaran.
• Garis lengkung: Himpunan seluruh titik yang membentuk garis lengkung yang menjadi keliling lingkaran.
• Diameter (d): garis yang ditarik oleh dari dua titik pada garis lengkung dan melewati titik pusat disebut sebagai diameter (d). Diameter lingkaran memiliki panjang 2 × r.
• phi (π): nilai perbandingan antara keliling serta diameter lingkaran selalu konstan yakni 3,14159 (dibulatkan menjadi 3,14) atau 22/7. Nilai ini didapatkan dari Keliling ÷ Diameter = phi.

Sifat-Sifat Lingkaran

• Memiliki simetri putar tak terhingga.
• Memiliki simetri lipat dan juga sumbunya yang tak terhingga.
• Lingkaran tidak memiliki titik sudut.
• Terdiri dari satu buah sisi.

Rumus Lingkaran

Nama	Rumus
Luas	L = π × r × r
	L = ¼ × π × d × d
Keliling	K = π × d
	K = π × 2r
phi	π = 22/7
	π = 3,14
Jari-jari	r = d/2
Diameter	d = 2r

Keterangan

• L = Luas
• K = Keliling
• π = 22/7 atau 3,14
• r = jari-jari
• d = diameter

Contoh Soal

Jika suatu lingkaran memiliki jari-jari sepanjang 21 cm, berapakah keliling dan luas lingkaran tersebut?

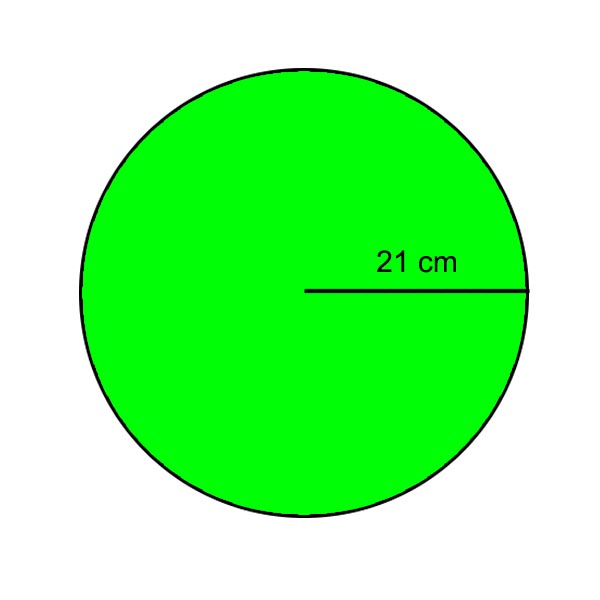
Penyelesaian

K = π × 2r
K = 22/7 × 2 × 21
K = 22 × 2 × 3
K = 22 × 6
K = 132 cm

L = π × r × r
L = 22/7 × 21 × 21
L = 22 × 3 × 21
L = 66 × 21
L = 1386 cm²

Jadi, keliling lingkaran tersebut adalah 132 cm dan luasnya adalah 1386 cm².

Demikianlah pembahasan lengkap mengenai bangun datar dan rumus-rumusnya. Semoga bermanfaat dan menambah wawasan kita semua.