Bilangan

Dalam pelajaran matematika, pasti berkaitan erat dengan yang namanya bilangan. Apa itu bilangan? Apa saja macam atau jenis bilangan? Berikut ini penjelasan lengkapnya.

Pengertian Bilangan

Bilangan adalah sesuatu yang memiliki nilai satuan, puluhan, ratusan, ribuan dan seterusnya. Atau bisa disebut, bilangan merupakan konsep matematika yang digunakan untuk pencacahan dan pengukuran.

Untuk menuliskan suatu bilangan kita dapat menggunakan lambang atau simbol yang lebih dikenal dengan angka.

Jenis Bilangan

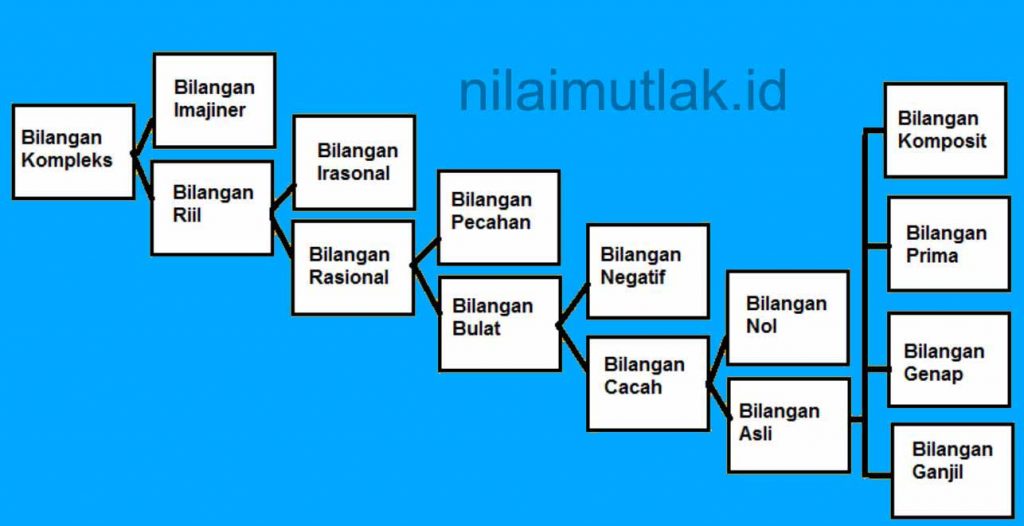
Konsep bilangan sudah bertahun-tahun lamanya, dan sudah diperluas menjadi beberapa jenis bilangan. Berikut ini macam-macam bilangan yang dikenal dalam matematika beserta anggota-anggotanya, antara lain :

Bilangan Prima

Bilangan prima adalah himpunan bilangan yang hanya memiliki dua faktor yaitu 1 dan bilangan itu sendiri. Bilangan ini jika dibagi dengan bilangan lain, maka hasilnya bukan bilangan bulat.

Contoh bilangan prima : P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, . . . .}

Bilangan Komposit

Bilangan komposit adalah himpunan bilangan yang memiliki tiga faktor atau lebih. Jadi ketika bilangan ini dibagi oleh salah satu faktornya, maka hasilnya tetap berupa bilangan bulat.

Contoh bilangan komposit : K = {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, . . . .)

Bilangan Genap

Bilangan genap adalah himpunan bilangan yang habis jika dibagi dengan 2. Atau bisa diartikan bahwa bilangan yang ketika dibagi 2, maka hasilnya tetap berupa bilangan bulat.

Contoh : Ge = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, . . . . }

Bilangan Ganjil

Bilangan ganjil adalah himpunan bilangan yang tidak habis jika dibagi dengan 2. Atau bisa dikatakan bahwa bilangan yang ketika dibagi dengan 2, maka hasilnya bukan bilangan bulat.

Contoh : Ga = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, . . . .}

Bilangan Asli

Bilangan asli adalah himpunan bilangan bulat yang dimulai dari satu dan seterusnya ke atas. Sehingga nilainya selalu positif.

Contoh : A = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, . . . .}

Bilangan Nol

Bilangan nol adalah bilangan nol itu sendiri.

Contoh : X = {0}

Bilangan cacah

Bilangan cacah adalah himpunan bilangan yang anggotanya terdiri dari bilangan nol dan bilangan asli. Sehingga tidak ada bilangan negatif.

Bilangan Negatif

Bilangan negatif adalah himpunan bilangan yang memiliki nilai kurang dari nol atau bisa ditulis < 0. Namun nol tidak termasuk dalam bilangan negatif.

Contohnya : T = {. . . ., -5, -4, -3, -2, -1, -¾, -½, -¼, . . }

Bilangan Positif

Bilangan positif adalah himpunan bilangan yang memiliki nilai lebih dari nol atau bisa ditulis > 0. Namun nol tidak termasuk dalam bilangan positif.

Contohnya : M = {. . . . ¼, ½, ¾, 1, 2, 3, 4, 5, 6}

Bilangan Bulat

Bilangan bulat adalah himpunan bilangan yang terdiri dari bilangan bulat negatih, nol, dan bilangan positif.

Contoh : N = { . . . ., -5, -4, -2, -1, 0, 1, 2, 3, 4, 5, . . .}

Bilangan Pecahan

Bilangan pecahan adalah himpunan yang memiliki pembilang dan penyebut.

Contohnya : D = {. . . ., -¾, -¼, -½, ¼, ½, ¾, 4/5, . . . .}

Bilangan Rasional

Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk pecahan atau a/b. Dengan catatan a dan b adalah bilangan bulat dan bukan nol ( ≠ 0 ).

Contohnya Q = {. . . ., -¾, -¼, -½, ¼, ½, ¾, 4/5, . . . .}

Bilangan Irrasional

Bilangan irrasional adalah himpunan bilangan real yang tidak dapat dituliskan atau diubah bentuknya menjadi bilangan pecahan.

Contoh : I = {. . . , √½, √2, √3, √5, √6, √7, . . . }

Bilangan Riil / Real

Bilangan real adalah himpunan bilangan yang terdiri dari bilangan negatif, nol, dan bilangan positif. Bilangan real ini juga dapat dinyatakan dalam bentuk desimal.

Contoh : R = {. . ., -2, -1, -¾, -½, -¼, 0, ¼, ½, ¾, 4/5, √2, √3, √5, √6, log 10, . . .}

Bilangan Imajiner

Bilangan imajiner adalah bilangan yang memuat nilai i yang mana jika i² = -1. Dalam bilangan imajiner tidak mengenal dengan adanya urutan.

Contoh : I = { i, 2i, 3i, 4i, ¼i, ½i, ¾i,. . .}

Bilangan Kompleks

Bilangan kompleks adalah bilangan yang terdiri dari bilangan riil dan bilangan imajiner. Bisa dinotasikan dengan (a + bi), yang mana a dan b adalah bilangan real dan i adalah bilangan imajiner.

Contoh : C = {3 + i, 5+ 2i, 0+i, 20-i, . . . }

Demikianlah pembahasan lengkap mengenai pengertian dan jenis-jenis bilangan serta anggota-anggotanya. Semoga informasi ini bermanfaat dan menambah wawasan kita semua.