Materi himpunan matematika merupakan salah satu materi dasar yang harus dikuasai temen-temen sekalian.
Pada materi ini kita akan dikenalkan dengan pengertian dari himpunan, jenis-jenisnya, contoh soal dan pembahasannya. Lebih jelasnya, silahkan simak pembahasan berikut ini.
Daftar isi
Pengertian Himpunan
Agar kita gampang memahaminya, coba teman-teman sebutkan contoh-contoh hewan yang hidup di air.
Misalkan hewan air itu ada lumba-lumba, paus, udang dan kerang. Kumpulan hewan-hewan tersebut bisa kita sebut sebagai himpunan hewan yang hidup di air.
Kemudian contoh hewan-hewan yang hidup di darat. Seperti singa, kerbau, sapi, kucing, dan kelinci. Kumpulan hewan tersebut bisa kita sebut sebagai himpunan hewan yang hidup di darat.
Lalu contoh hewan yang memiliki dua kaki. Ada ayam, bebek, angsa, dan kanguru. Kumpulan hewan tersebut bisa kita sebut sebagai himpunan hewan yang memiliki dua kaki.
Sekarang bagaimana kalau himpunan nama bulan dalam setahun yang terdiri dari 32 hari? Sudah tentu tidak ada kan. Wah, terus bagaimana cara menuliskan himpunan yang tidak memiliki anggota? Nanti akan kita bahas.
Dari beberapa contoh di atas dapat kita simpulkan definisi himpunan
Sekarang coba deh perhatikan beberapa kumpulan berikut ini!
- Kumpulan laki-laki berparas ganteng
- Kumpulan bilangan cacah
- Kumpulan orang yang rajin
- Kumpulan bilangan bulat positif
Dari contoh kumpulan di atas, bisakah kalian bedakan mana yang merupakan himpunan dan yang bukan himpunan?
Jika diperhatikan dengan seksama, contoh yang merupakan himpunan adalah contoh ke 2 dan ke 4. Sedangkan contoh ke 1 dan ke 3 bukan himpunan. Apa kalian tahu alasannya?
Bila kalian masih bingung, perhatikan alasan berikut.
Pada contoh ke 2 himpunan bilangan cacah, kita akan memikirkan hal yang sama tentang bilangan berapa sajakah yang termasuk anggota bilangan cacah. Yaitu 0,1,2, dan 3. Dan kita semua setuju bahwa kalau bilangan tersebut termasuk bilangan cacah kan?
Pada contoh 1 laki-laki berparas ganteng dan contoh 3 orang yang rajin, keduanya tidak memiliki definisi yang jelas. Setiap orang memiliki definisi masing-masing tentang kata ganteng dan rajin.
Contoh gampangnya seperti ini misalnya Ani menganggap Bayu ganteng, tapi belum tentu Anggi menganggap Bayu ganteng juga, bukan? Begitu juga dengan kata rajin. Oleh karena itu, laki-laki dan orang yang rajin bukanlah suatu himpunan. Karena tidak dapat didefinisikan dengan jelas.
Nah, berdasarkan contoh kumpulan himpunan di atas, saya harap kalian udah tahu perbedaan himpunan dan bukan himpunan.
Sekarang kita akan belajar bagaimana cara menyatakan suatu himpunan dan macam-macam himpunan.
Cara Menyatakan Himpunan
Setelah teman-teman memahami pengertian dari himpunan, sekarang kita belajar memahami cara untuk menyatakan suatu himpunan.
Secara umum, himpunan dapat disimbolkan dengan huruf kapital. Jika anggota himpunan tersebut berupa huruf, maka anggotanya dituliskan dengan huruf kecil. Ada 3 cara yang dapat digunakan untuk menyatakan suatu himpunan, yaitu :
1. Menyebutkan sifat yang dimiliki anggota-anggotanya
Yaitu dengan menyebutkan sifat yang dimiliki setiap anggotanya secara spesifik.
Contoh : A merupakan himpunan bilangan genap antara 2 dan 10
Dapat ditulis menjadi
A = { bilangan genap antara 2 dan 10}
Dari sifat yang disebutkan, kita dapat mengetahui anggota himpunan A yaitu 4, 6 dan 8
2. Menyebutkan anggota-anggotanya
Jika dengan menyebutkan anggotanya, maka menggunakan penulisan seperti ini.
Contoh : A = { 4, 6, 8 }
3. Menggunakan notasi pembentuk himpunan
yaitu menyebutkan semua sifat dari anggota himpunan dengan anggotanya yang dinyatakan dalam suatu variabel dan dituliskan di dalam kurung kurawal.
Contoh : A = { x | 2 < x < 10, x ∈ bilangan genap}
Cara baca : “Himpunan A adalah himpunan yang anggotanya adalah x sedemikian sehingga 2 lebih kecil dari x dan x lebih kecil dari 10, dengan x adalah bilangan genap”
Mungkin teman-teman sekalian masih ada yang bingung, apakah semua himpunan dapat dinyatakan dengan ketiga cara tersebut?
Jawabannya tentu saja tidak. Karena tidak semua himpunan bisa kita ditulis dengan menyebutkan semua anggotanya.
Contohnya saja himpunan bilangan real (riil) yang tidak bisa disajikan dengan menyebutkan semua anggotanya. Sehingga lebih cocok dinyatakan dengan cara notasi pembentuk himpunan.
Biar makin paham, simak contoh soal berikut ini.
Contoh Soal
Tulislah himpunan berikut dengan cara menyebutkan anggota nya dan notasi pembentuk himpunan!
- B = {bilangan ganjil antara 4 dan 20 }
- C = {bilangan cacah kurang dari 9}
Pembahasan nomor 1
Bilangan ganjil adalah bilangan asli yang bukan kelipatan dari 2 dan tidak habis dibagi 2. Jadi, anggota himpunan B adalah 5,7,9,11, 13, 15, 17, dan 19. Sehingga dapat ditulis
B = {5, 7, 9,11, 13, 15, 17, 19}
Atau
B = { x | 4 < x < 20, x ∈ bilangan ganjil}
Pembahasan nomor 2
Bilangan cacah merupakan bilangan bulat yang tidak negatif yang dimulai dari angka 0. Jadi, anggota himpunan D adalah 0,1,2,3,4,5,6,7, dan 8. Sehingga dapat ditulis
C = {0, 1, 2, 3, 4, 5, 6, 7, 8}
Atau
0 = { x | 0 ≤ x < 9, x ∈ bilangan cacah}
Kardinalitas himpunan
kardinalitas himpunan adalah banyaknya anggota yang ada di dalam sebuah himpunan. Contoh adalah seperti ini:
A = {merah, kuning, biru, hijau}
maka kardinalitas himpunannya adalah 4 atau n(A) = 4
B = {4, 8, 12, 16, 20}
maka kardinalitas himpunannya adalah 5 atau n(B) = 5
C = {x│x < 10, x bilangan asli}
maka kardinalitas himpunannya adalah 9 atau n(C) = 9
karena anggota himpunan C = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Diagram Venn
Suatu himpunan dapat disajikan dengan cara menuliskan anggotanya dalam suatu gambar (diagram) yang dinamakan diagram Venn. Aturan dalam pembuatan diagram Venn adalah sebagai berikut:
- Menggambar sebuah persegi panjang untuk menunjukkan semesta dengan mencantumkan huruf S di pojok kiri atas.
- Setiap himpunan yang ada dalam himpunan semesta ditunjukkan oleh kurva tertutup sederhana.
- Memberi noktah (titik) berdekatan dengan masing-masing anggota himpunan. Untuk suatu himpunan anggotanya banyak sekali, maka noktah-noktah tidak perlu digambarkan
Untuk lebih jelasnya perhatikan contoh diagram venn berikut ini :
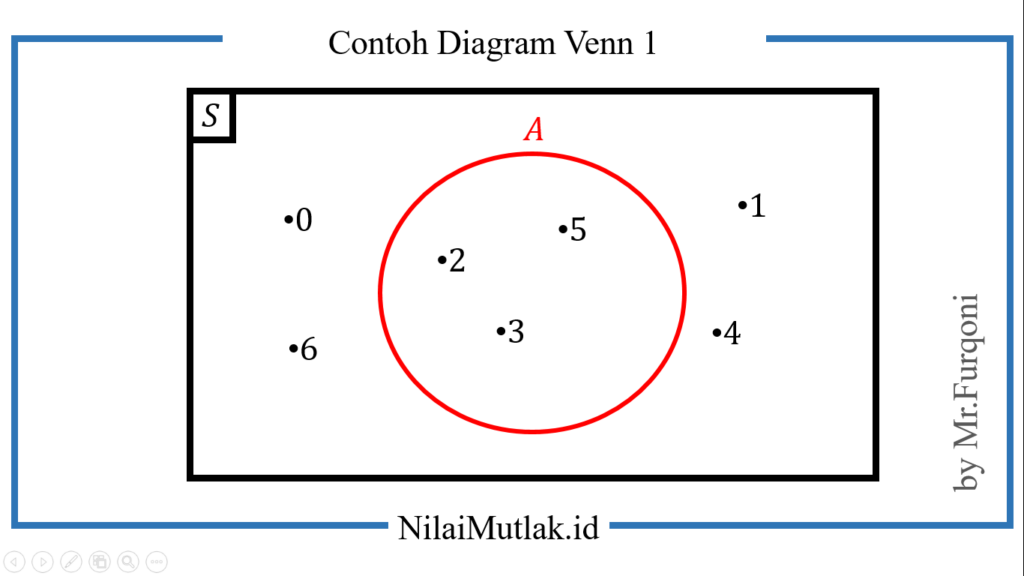
Contoh 1
Misalkan S = {0, 1, 2, 3, 4, 5, 6} adalah himpunan semesta, dan A = {2, 3, 5}. Maka bentuk diagram venn nya adalah sebagai berikut :
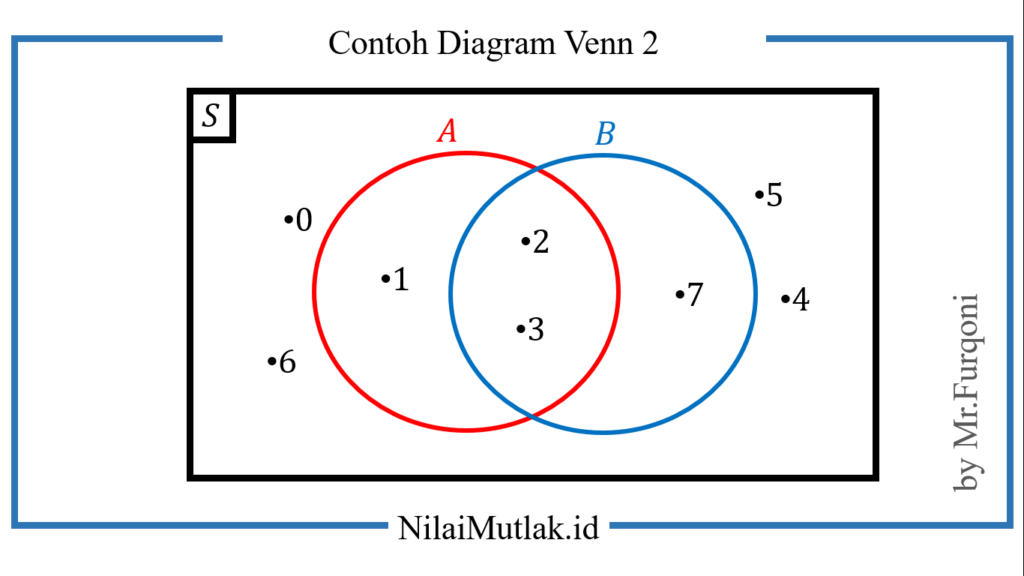
Contoh 2
Misalkan A = {1, 2, 3}, B = {2, 3, 7} dan himpunan semesta S = {0, 1, 2, 3, 4, 5, 6, 7}. Maka bentuk diagram venn nya adalah sebagai berikut
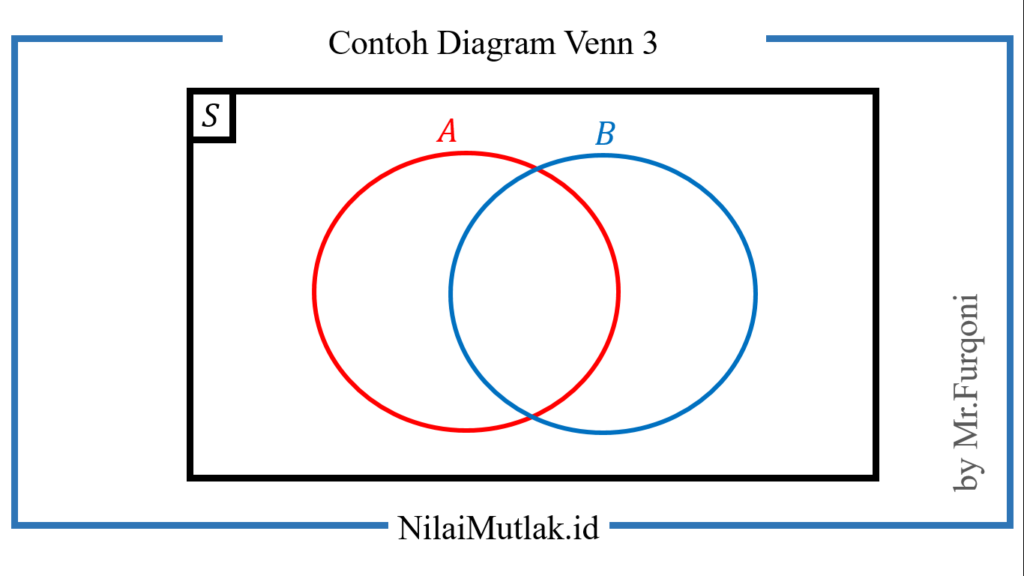
Contoh 3
Misalkan A = {bilangan genap}, B = {bilangan prima} dan himpunan semesta S = {bilangan asli}. Maka bentuk diagram venn nya adalah sebagai berikut
Jenis Himpunan
Dalam materi himpunan, ada beberapa jenis himpunan yang wajib kalian ketahui. Ada himpunan semesta, himpunan bagian, himpunan kosong, himpunan kuasa, dan lain-lain. Berikut pembahasannya
Himpunan Semesta
Himpunan semesta adalah himpunan seluruh unsur yang menjadi objek pembicaraan, dan dilambangkan dengan S. Himpunan semesta disebut juga semesta pembicaraan atau himpunan universal.
Untuk lebih jelasnya perhatikan contoh berikut ini!
Contoh 1
Sebutkan paling sedikit dua buah himpunan semesta yang mungkin dari himpunan
A = { 3, 5, 7 }
Penyelesaian :
Himpunan semesta dari himpunan A adalah { bilangan asli }, atau { bilangan ganjil }, atau { bilangan prima }, atau { bilangan cacah }.
Contoh 2
Sebutkan paling sedikit dua buah himpunan semesta yang mungkin dari himpunan
B = { Januari, Juli}
Penyelesaian
Himpunan semesta dari himpunan B adalah { nama-nama bulan }; atau { nama-nama bulan yang diawali dengan huruf J }; atau { nama-nama bulan yang jumlah harinya 31 hari}.
Himpunan kosong (∅)
Himpunan kosong merupakan suatu himpunan yang tidak memiliki anggota. Untuk lebih jelasnya, perhatikan contoh himpunan berikut ini!
Contoh 1
A = {Bilangan cacah yang kurang dari 0}
Anggota Bilangan cacah yang paling kecil adalah 0, sehingga himpunan tersebut C adalah himpunan yang tidak memiliki anggota.
Contoh 2
B = {Bilangan bulat yang lebih dari 4 dan kurang dari 5}
Tidak ada satupun bilangan asli antara 4 dan 5. Dengan demikian himpunan tersebut adalah himpunan yang tidak memiliki anggota.
Contoh 3
C = {Nama bulan yang lamanya 32 hari}
Tidak ada satupun bulan yang lamanya 32 hari. Dengan demikian himpunan tersebut yang diperoleh adalah himpunan yang tidak memiliki anggota.
Himpunan Bagian (Subset)
Himpunan bagian merupakan suatu himpunan yang seluruh anggotanya merupakan anggota dari himpunan lain. Untuk lebih jelasnya perhatikan diagram venn berikut:
Misalkan
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {0, 1, 2, 3, 4, 5, 6}
B = {0, 1, 2}
Maka bentuk diagram venn nya adalah sebagai berikut
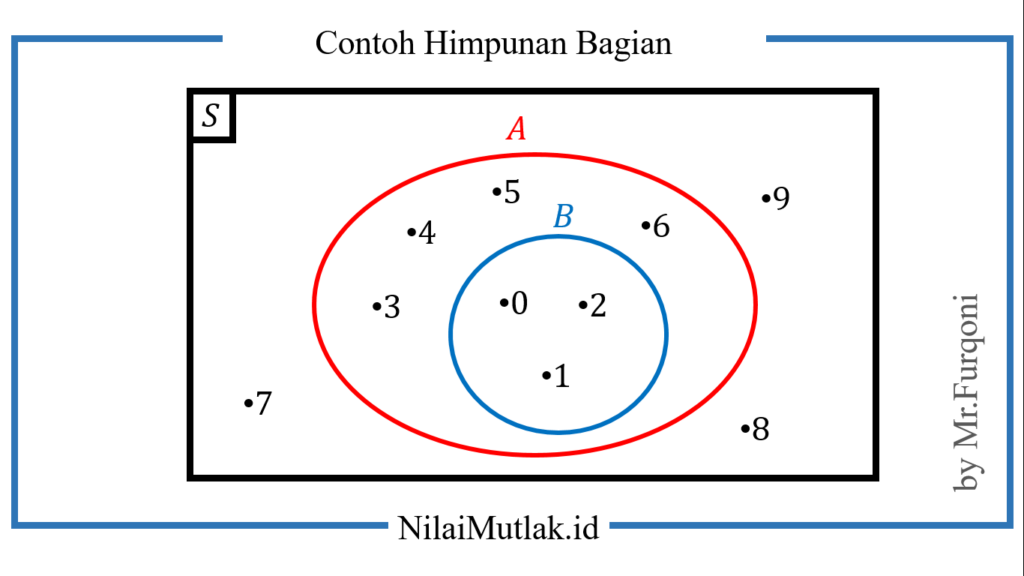
Penjelasan
- Coba Kamu amati diagram Venn gambar tersebut. Pada diagram Venn tersebut, himpunan B berada di dalam himpunan A. Dengan kata lain setiap anggota B juga merupakan anggota A. Hal ini dikatakan bahwa B adalah himpunan bagian dari A dan ditulis “A ⊂ B”.
- Pada diagram Venn tersebut, himpunan B berada di dalam himpunan S. Dengan kata lain setiap anggota B juga merupakan anggota S. Hal ini dikatakan bahwa B adalah himpunan bagian dari Sdan ditulis “B ⊂ S”.
- Pada diagram Venn tersebut, himpunan A tidak berada di dalam himpunan B, sebab ada anggota himpunan A yang bukan anggota himpunan B, yaitu 3, 4, 5, 6. Sehingga himpunan A bukan himpunan bagian dari himpunan B, ditulis dengan A ⊄ B.
Himpunan B merupakan himpunan bagian dari himpunan A jika setiap anggota himpunan B juga merupakan anggota himpunan A, dilambangkan B ⊂ A. Jika ada anggota A yang bukan anggota B, maka B bukan himpunan bagian dari A, maka bisa dilambangkan dengan B ⊄ A.
Himpunan Kuasa
Himpunan Kuasa dari himpunan M adalah himpunan dari semua himpunan bagian dari M, dinotasikan dengan P(M). Banyak anggota himpunan kuasa dari himpunan M dilambangkan dengan n(P(M)). Untuk lebih jelasnya perhatikan contoh berikut ini :
Diberikan himpunan M = {1, 2, 3}, carilah himpunan-himpunan yang merupakan himpunan bagian dari M !
Himpunan-himpunan yang merupakan himpunan bagian dari M adalah:
- Himpunan yang banyak anggotanya 0, yaitu: {} atau ∅
- Himpunan yang banyak anggotanya adalah 1, yaitu {1}, {2}, {3}
- Himpunan yang banyak anggotanya adalah 2, yaitu {1, 2}, {1, 3}, {2, 3}
- Himpunan yang banyak anggotanya adalah 3 adalah himpunan M itu sendiri,yaitu {1, 2, 3}
Berdasarkan uraian di atas himpunan yang anggotanya himpunan-himpunan bagian dari M adalah {{ }, {1}, {3}, {5}, {1, 3}, {1, 5}, {3, 5}, {1, 3, 5}}. Himpunan ini dinamakan himpunan kuasa dari M, dinotasikan dengan P(M). Jadi, P(M) = {{ }, {1}, {3}, {5}, {1, 3}, {1, 5}, {3, 5},{1, 3, 5}} Banyak himpunan kuasa M adalah 8, ditulis n(P(M)) = 8.
Untuk menentukan jumlah himpunan kuasa, perhatikan tabel berikut :
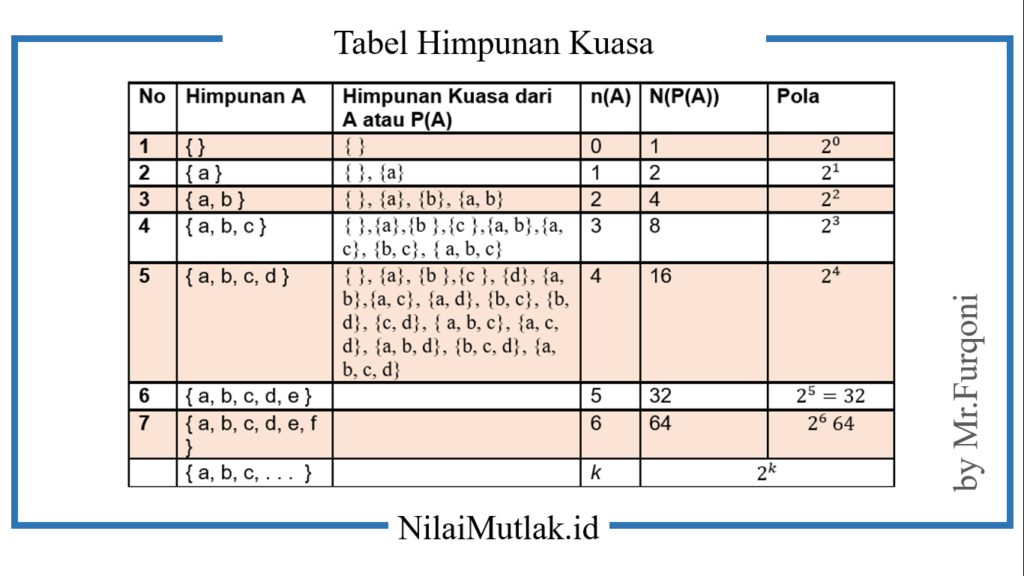
Sehingga dapat dikatakan bahwa Misalkan A himpunan dan P(A) adalah himpunan kuasa dari A. Jika n(A) = k, dengan k bilangan cacah, maka n(P(A)) = 2^k.
Kesamaan dua himpunan
Dua himpunan P dan Q dikatakan sama jika dan hanya jika P ⊂ Q dan Q ⊂ P. Dilambangkan P = Q. Atau bisa dibilang bahwa dua himpunan dikatakakan sama apa bila kedua himpunan tersebut secara keseluruhan memiliki anggota yang sama.
Untuk lebih jelasnya perhatikan contoh berikut
Diketahui himpunan P = {2, 3, 5} dan Q = {bilangan prima kurang dari 7 }.
Dari kedua himpunan tersebut, kita harus menyelidiki bilangan mana saja yang menjadi anggotanya.
P = {2, 3, 5} dan Q = {2, 3, 5}.
Jika digambar dalam diagram venn, Maka hasilnya adalah seperti ini
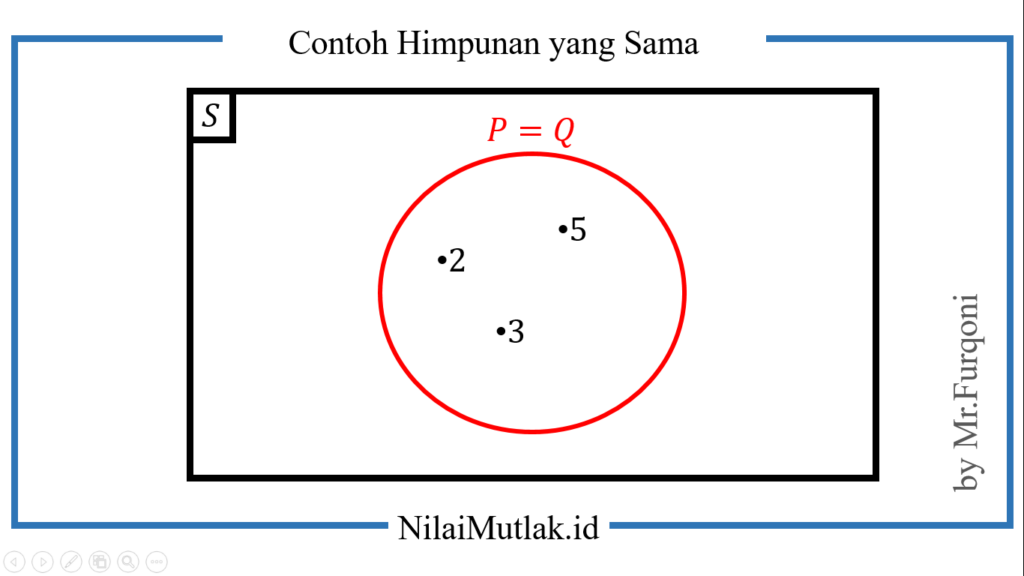
Karena semua anggota himpunannya sama, maka terbukti bahwa P ⊂ Q dan Q ⊂ P. Sehingga dapat disimpulkan bahwa P = Q
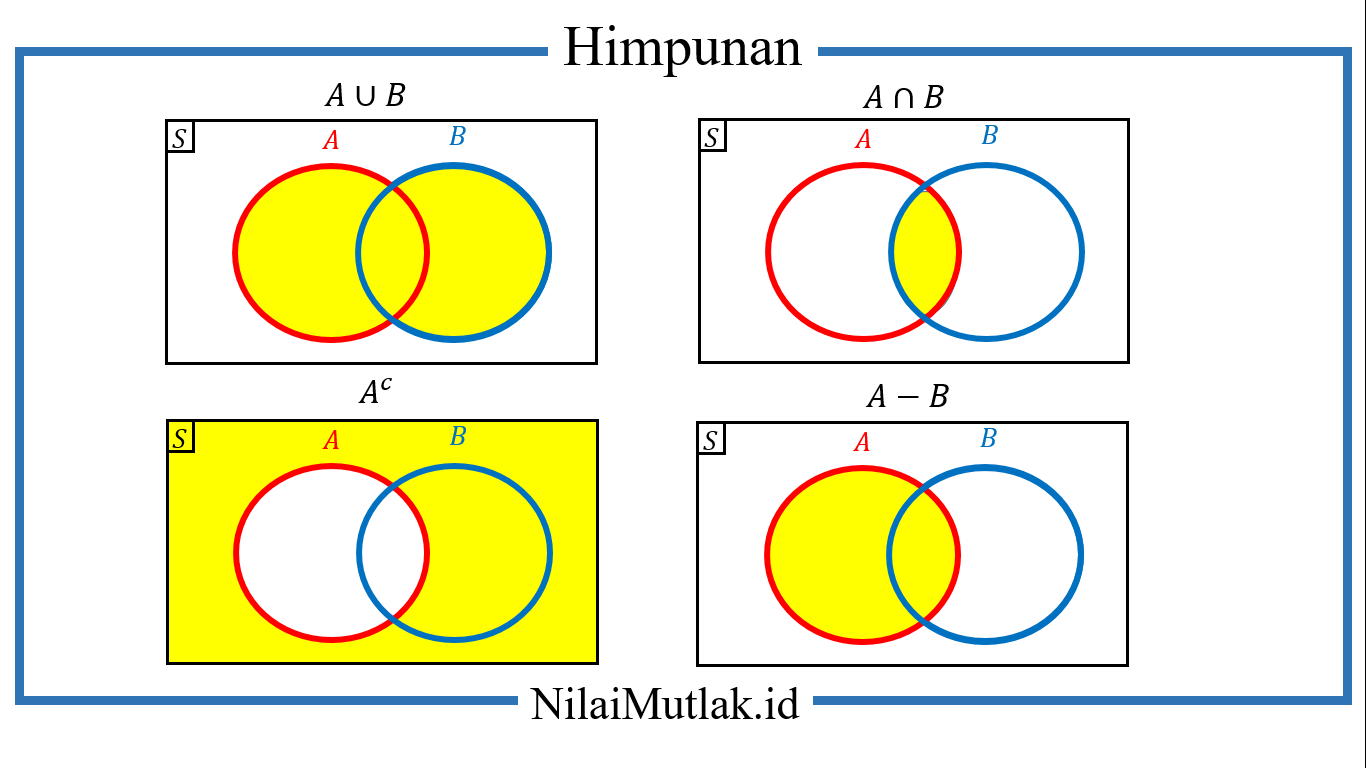
Operasi Himpunan
Okay selanjutnya kita akan bahas tentang operasi himpunan nih. Ada irisan, gabungan dan komplemen. Seperti apa operasinya, simak penjelasan berikut ini!
Irisan
Irisan himpunan A dan B adalah himpunan semua anggota yang merupakan anggota himpunan A dan himpunan B. Dilambangkan A ∩ B = {x│x ∈ A dan x ∈ B}.
Contoh 1
A = { 7, 8, 9, 10 } dan B = { 6, 7, 9 }
Maka A ∩ B = {7, 9}
Jika digambar dalam diagram venn maka hasilnya seperti ini
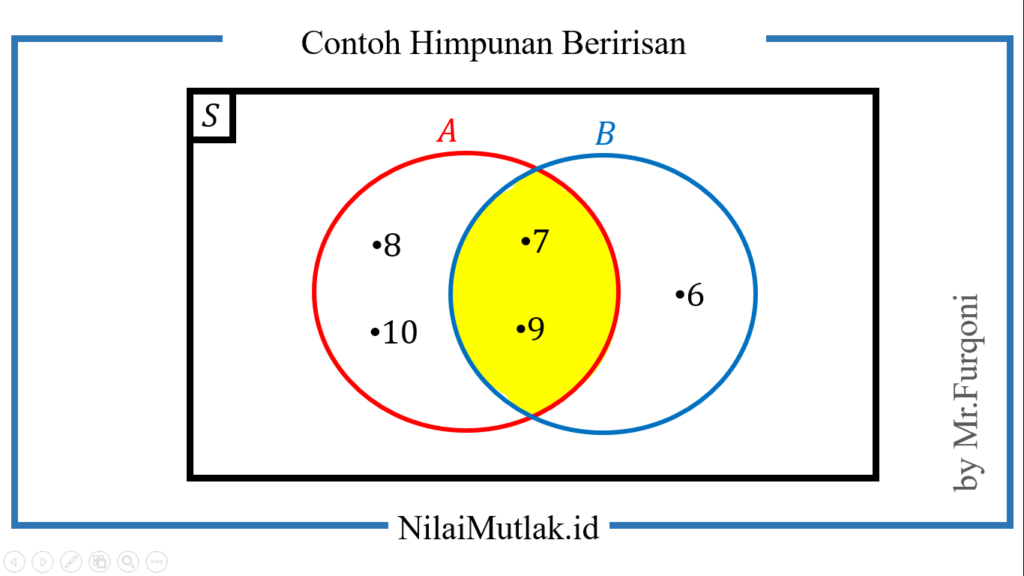
Hubungan antara himpunan A dan B adalah dua himpunan yang saling beririsan atau tidak saling lepas.
Contoh 2
C = { 0, 3, 6 } dan D = { 1, 2, 5 }
Maka C ∩ D = { }
Jika digambar dalam diagram venn maka hasilnya seperti ini
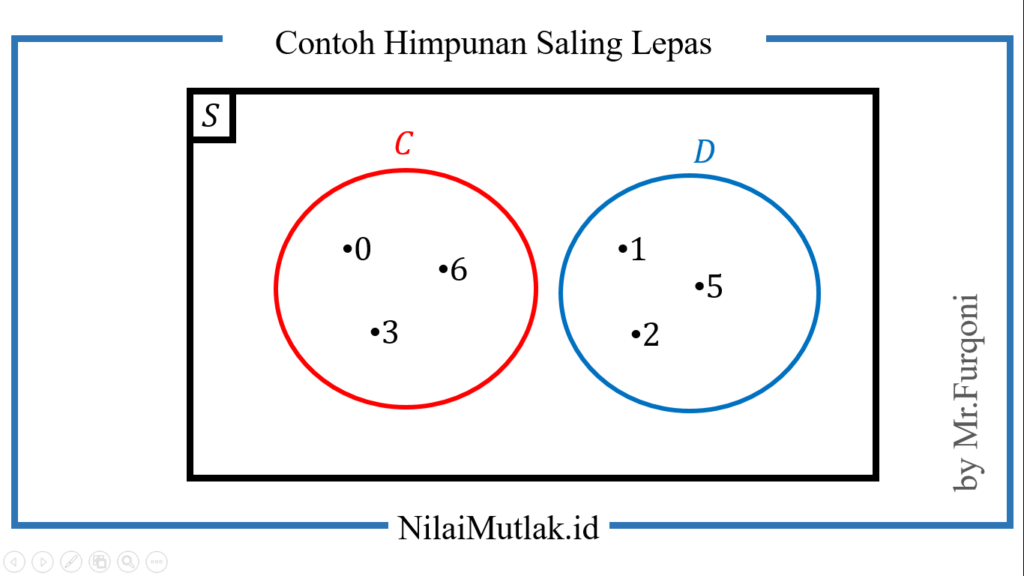
Karena tidak ada elemen himpunan C yang ada di himpunan D, maka kita sebut irisan himpunan C dan himpunan D adalah himpunan kosong, di lambangkan dengan C ∩ D = Ø atau C ∩ D = { } Jika C ∩ D = Ø disebut bahwa himpunan C saling lepas dengan himpunan D.
Catatan :
Himpunan C dan D dikatakan saling lepas atau saling asing, jika tidak ada anggota C yang merupakan anggota D dan tidak ada anggota D yang merupakan anggota C. Dinotasikan dengan C // D
Contoh 3
E = { 4, 6 } dan F = { 2, 4, 6 }
Maka E ∩ F = { 4, 6 }
Jika digambar dalam diagram venn maka hasilnya seperti ini
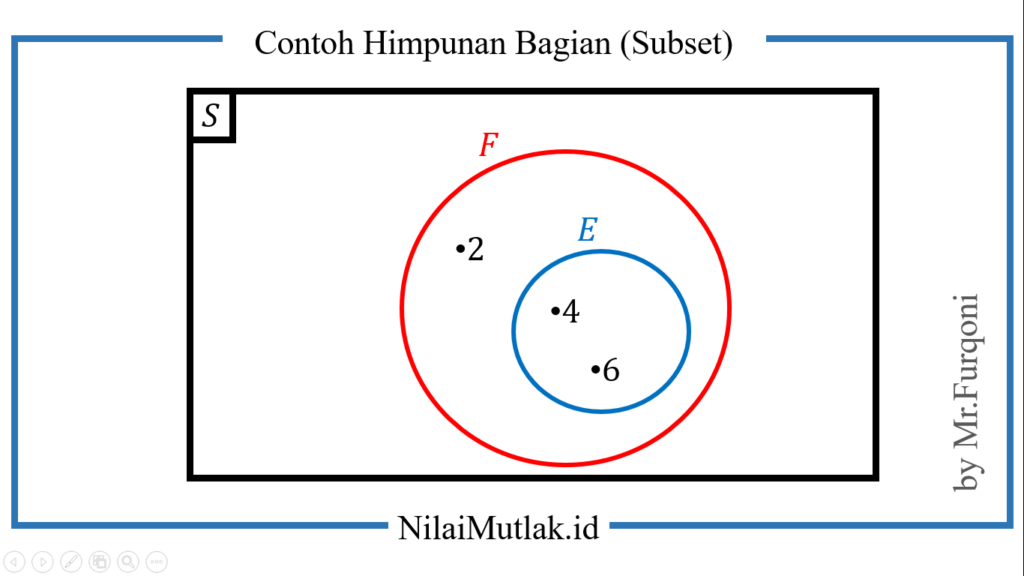
Karena seluruh anggota himpunan E merupakan anggota himpunan F,
maka disimpulkan E ⊂ F dan E ∩ F = E.
Gabungan
Gabungan himpunan A dan B adalah himpunan yang anggotanya merupakan anggota himpunan A atau anggota himpunan B, dilambangkan dengan A ∪ B.
A ∪ B = {x | x ∈ A atau x ∈ B}
Jika digambar dalam diagram venn, maka hasilnya adalah seperti ini
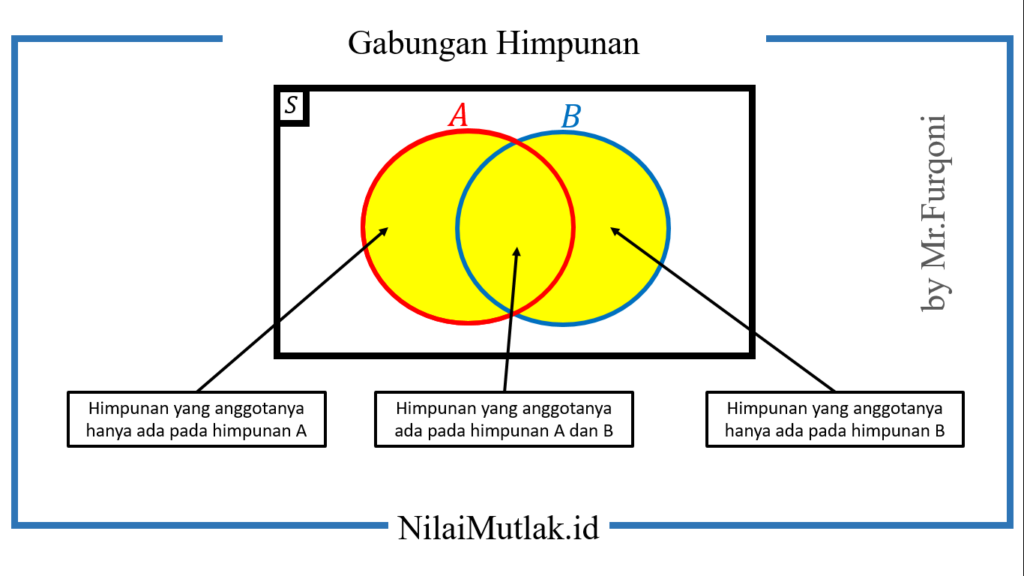
Untuk lebih jelasnya, simak contoh berikut ini!
Contoh 1
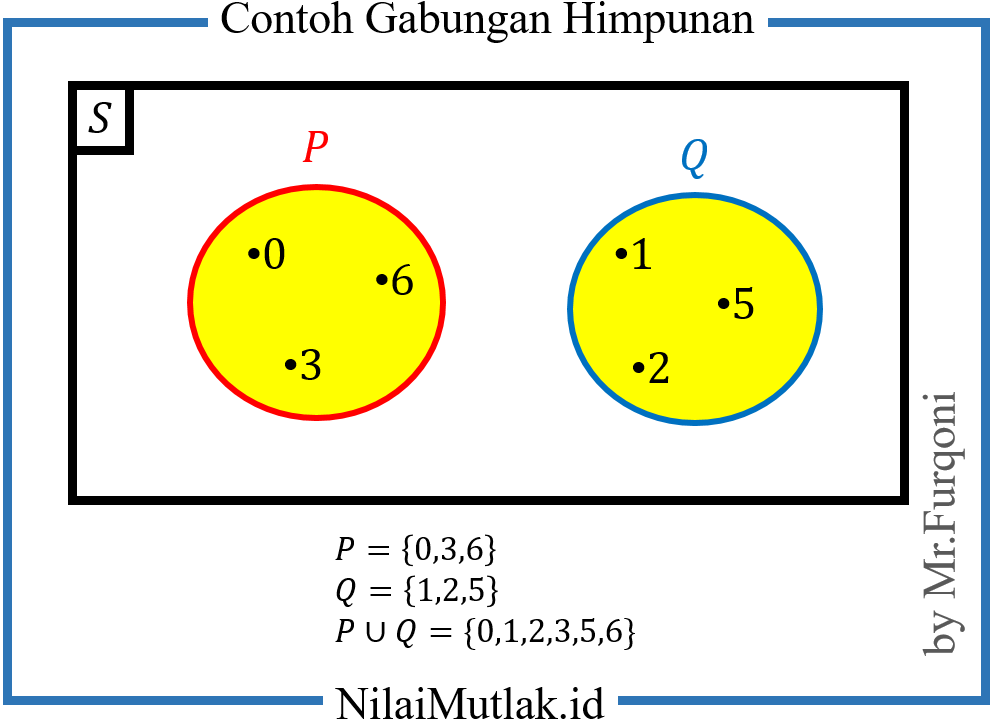
P = {0, 3, 6} dan Q = {1, 2, 5}
P ∪ Q = himpunan semua anggota yang ada di P digabungkan dengan semua anggota di Q
P ∪ Q = {0, 3, 6, 1, 2, 5}
P ∪ Q = {0, 1, 2, 3, 5, 6}
Contoh 2
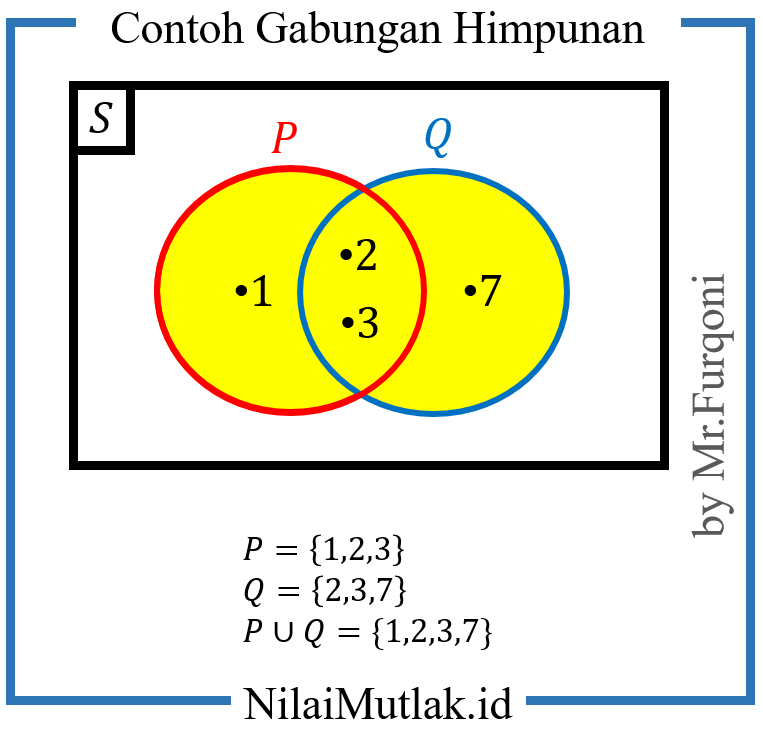
P = {1, 2, 3}, Q = {2, 3, 7}
Maka P ∪ Q = {1, 2, 3, 7}
Catatan :
Perhatikan kardinalitas himpunannya.
Jika himpunannya saling lepas maka kardinalitas himpunannya
n(A ∪ B)= n(A) + n(B)
Jika himpunannya saling beririsan maka kardinalitas himpunannya
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Komplemen Himpunan
Misalkan S adalah himpunan semesta dan A adalah suatu himpunan. Komplemen himpunan A adalah suatu himpunan semua anggota himpunan S yang bukan anggota himpunan A, dilambangkan dengan Ac . Dengan notasi pembentuk himpunan definisi ini dapat dituliskan sebagai berikut. Ac = {x | x ∈ S dan x ∉ A}
Contoh 1
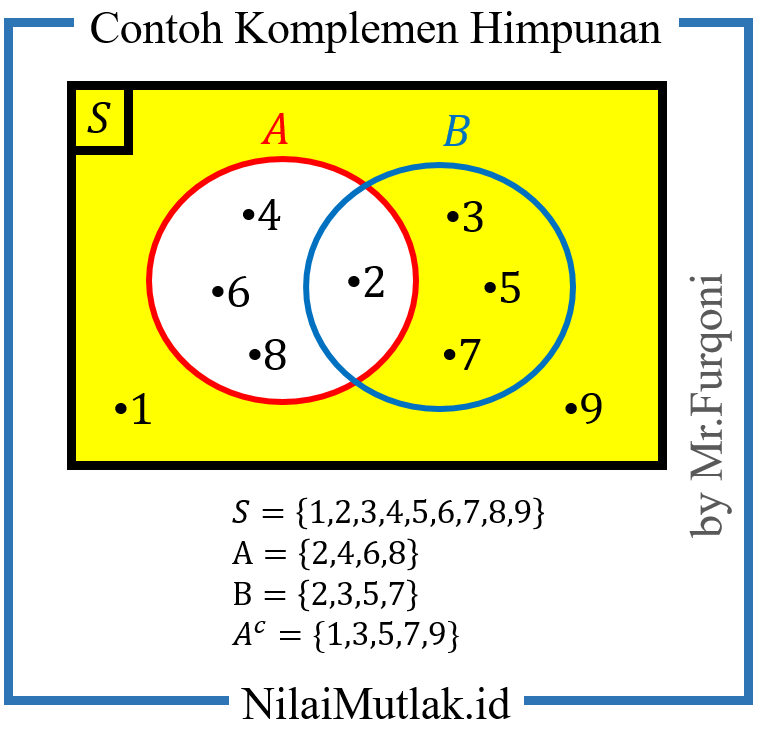
S = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {2, 4, 6, 8}
Maka Ac adalah = { 1, 3, 5, 7, 9 }
Contoh 2
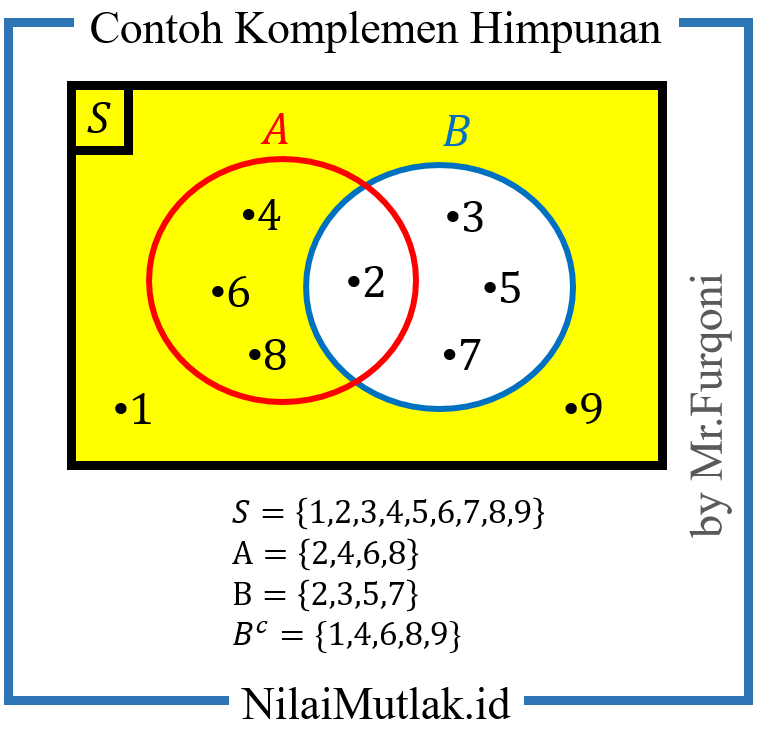
S = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {2, 4, 6, 8}
B = {2, 3, 5, 7}
Maka Bc adalah = { 1, 4, 6, 8, 9 }
Misalkan S himpunan semesta dan P ⊂ S , maka :
1. P ∩ Pc = Ø
2. P U Pc = S
3. n(P) + n(Pc) = n(S)
Misalkan S himpunan semesta dan P ⊂ S , maka :
1. (P ∩ Q)c = Pc U Qc
2. (P U Q)c = Pc ∩ Qc
Selisih Himpunan
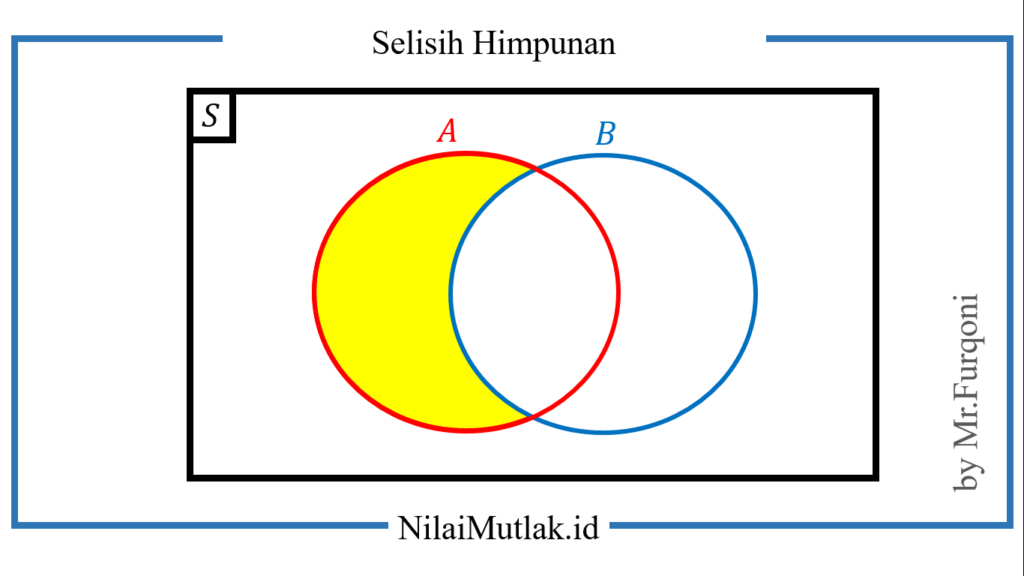
Selisih B terhadap A adalah himpunan semua anggota himpunan A yang bukan anggota himpunan B, dilambangkan dengan A – B. Ditulis : A – B = {x | x ∈A dan x ∉ B} = A ∩ Bc
Jika digambar dalam diagram venn maka hasilnya seperti ini
Contoh 1
S = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 }
A = { 2, 4, 6, 8, 10, 12, 14 }
B = { 3, 6, 9, 12, 15 }
Maka
A – B = { 2, 4, 8, 10, 14 }
Jika digambar dengan diagram venn, maka hasilnya seperti ini
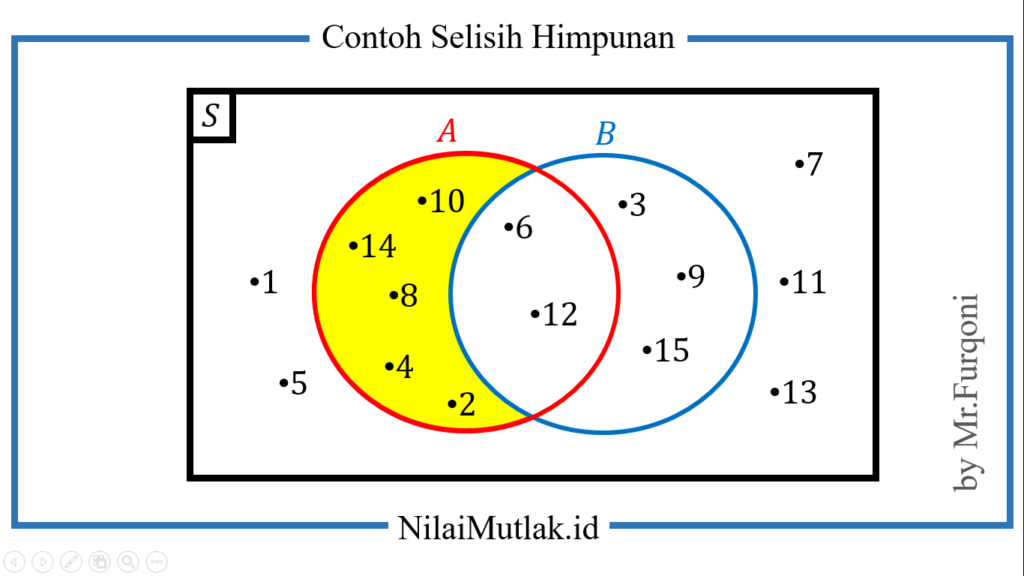
Contoh 2
S = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 }
A = { 2, 4, 6, 8, 10, 12, 14 }
B = { 3, 6, 9. 12, 15 }
Maka
B – A = { 3, 9, 15 }
Jika digambar dengan diagram venn, maka hasilnya seperti ini
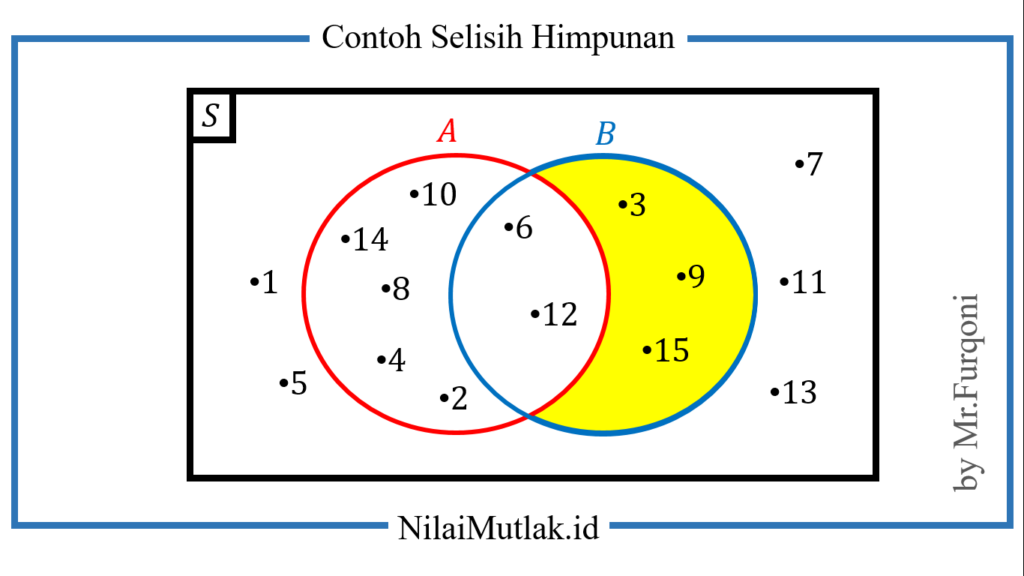
Untuk sembarang himpunan A dan B, berlaku:
Jika A ∩ B = ∅, maka A – B = A dan B – A = B
Jika A ⊂ B, maka A – B = ∅
Sifat Operasi Himpunan
Perlu kalian ketahui ada beberapa sifat operasi pada himpunan, antara lain :
Sifat Komutatif
Misalkan A dan B adalah himpunan:
1. A ∪ B = B ∪ A
2. A ∩ B = B ∩ A
Sifat Asosiatif
Untuk sembarang himpunan P, Q, dan R, berlaku:
1. (P ∪ Q)∪ R = P ∪ (Q ∪ R)
2. (P ∩ Q) ∩ R = P ∩ (Q ∩ R)
3. P ∪ (Q ∩ R) = (P ∪ Q) ∩ (P ∪ R)
4. P ∩ (Q ∪ R) = (P ∩ Q) ∪ (P ∩ R)
Untuk sebarang himpunan A, B, dan C, berlaku sifat-sifat:
Sifat komplemen
(A ∪ B)c = Ac ∩ Bc
(A ∩ B)c = Ac ∪ B c
(Ac) c = A
Sifat identitas
A ∪ Ø = A
A ∩ Ø = Ø
Sifat idempoten
A ∪ A = A
A ∩ A = A
Sifat distributif
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
1) Himpunan kosong (Ø) merupakan himpunan bagian dari semua himpunan.
2) Jika n(A) = k, maka n(P(A)) = 2 k , k bilangan bulat positif.
3) Jika A ⊂ B maka A ∩ B = A.
4) Jika A ∩ B = Ø maka A – B = A dan B – A = B.
5) Jika A ⊂ B, maka A – B = Ø.
6) n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
7) n (A ∪ B ∪ C) = n (A) + n (B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n (A ∩ B ∩ C).
8) Jika A ⊂ B maka A ∪ B = B
Okay temen-temen. Mungkin cukup sekian pembahasan lengkap terkait dengan materi himpunan matematika. Semoga bermanfaat. Terimakasih. Selamat Belajar.

Seorang mahasiswa pendidikan matematika di Universitas Muhammadiyah Purwokerto yang suka bermain dengan logika. Founder teknikece.com