Mean Median Modus

Untuk mendapatkan gambaran yang lebih jelas mengenai suatu kumpulan data tidak hanya menggunakan tabel atau diagram saja. Tetapi juga diperlukan ukuran-ukuran. Kali ini akan bahas lebih dalam tentang ukuran pemusatan data.

Beberapa ukuran yang termasuk dalam ukuran pemusatan data adalah rata-rata hitung (mean), modus dan median. Ukuran pemusatan menunjukkan di mana suatu data memusat atau suatu kumpulan pengamatan memusat.

Mean atau Rata-Rata Hitung

Untuk Data Tunggal

Jika diketahui sebanyak n data tunggal, maka rata-ratanya adalah jumlah seluruh data dibagi dengan banyaknya data.

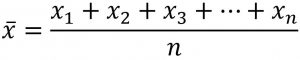
atau

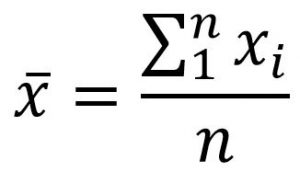
Keterangan:

[latex] \bar x [/latex] : rata-rata

[latex] x_i [/latex] : data ke i

n : banyaknya data

Contoh

Tentukan rata-rata skor ulangan dari 10 siswa di bawah ini.

6, 7, 8 , 6, 8, 5, 6, 9, 7, 6

Penyelesaian

[latex] \bar x = \frac{\sum_{1}^{n} x_{i}}{n} = \frac{6+7+8+6+8+5+6+9+7+6}{10} = \frac{67}{10} = 6,7[/latex]

Jadi, rata-rata skor ulangan 10 siswa tersebut adalah 6,7.

Jika data tunggal tersebut disajikan dalam tabel distribusi frekuensi, maka rata-ratanya dapat ditentukan sebagai berikut.

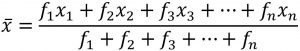
atau

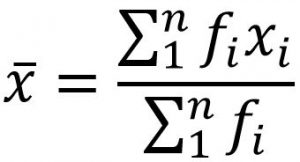
Contoh

Berikut ini adalah data rata-rata skor ulangan dari 10 siswa pada contoh sebelumnya yang disajikan dalam tabel distribusi frekuensi.

[table id=32 /]

Dari data di atas, tentukan rata-ratanya.

[latex] \bar x = \frac {\sum_{1}^{n} f_{i} x_{i}}{\sum_{1}^{n} f_{i}} = \frac{67}{10} = 6,7[/latex]

Jadi, rata-rata skor ulangan 10 siswa tersebut adalah 6,7.

Untuk Data Berkelompok

Untuk menentukan rata-rata data berkelompok, pada prinsipnya sama dengan menentukan rata-rata data tunggal. Seperti yang disajikan dalam tabel distribusi frekuensi, perbedaanya hanya pada nilai [latex]x_{i}[/latex].

Saat menentukan rata-rata data tunggal yang disajikan dalam tabel distribusi frekuensi [latex]x_{i}[/latex] menyatakan data ke [latex]i[/latex], sedangkan pada data berkelompok [latex]x_{i}[/latex] menyatakan titik tengah dari suatu interval tertentu. Perhatikan contoh berikut.

Di bawah ini adalah data nilai ujian mata pelajaran matematika dari 80 orang siswa. Dari data tersebut akan ditentukan rata-rata skor ujian akhirnya.

[table id=33 /]

Penyelesaian

[table id=34 /] [latex] \bar x = \frac {\sum_{1}^{n} f_{i} x_{i}}{\sum_{1}^{n} f_{i}} = \frac{6070}{80} = 75,875[/latex]

Jadi, rata-rata skor UAS matematika adalah 75,88.

Modus

Modus merupakan nilai yang mewakili fenomena yang paling banyak terjadi. Sehingga modus dari suatu data adalah datum yang paling sering muncul atau datum yang memiliki frekuensi tertinggi.

Dalam menentukan modus suatu data bisa terdapat

• satu modus (unimodus),
• dua modus (bimodus),
• lebih dari dua modus (multimodus), dan
• sama sekali tidak memiliki modus.

Data dikatakan tidak memiliki modus jika frekuensi semua datum sama.

Modus data tunggal

Contoh : Tentukan modus dari data tunggal di bawah ini.

[table id=35 /]

Penyelesaian

Modus dari data di atas 6, karena skor 6 mempunyai frekuensi terbanyak, yaitu 8.

Modus Data Berkelompok

Modus yang sesungguhnya dari data berkelompok sebenarnya tidak dapat dicari. Sehingga ditetapkan aturan bahwa suatu kelas yang memiliki frekuensi tertinggi disebut kelas modus.

Modus dari data berkelompok adalah suatu nilai dalam kelas modus yang ditentukan dengan rumus sebagai berikut.

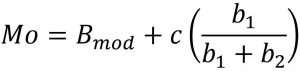
Keterangan:

[latex] Mo [/latex] = modus

[latex] B_{mod} [/latex] = batas bawah kelas modus (kelas yang memuat modus)

[latex] c [/latex] = panjang interval kelas modus

[latex] b_1 [/latex] = selisih frekuensi kelas modus dengan kelas sebelumnya.

[latex] b_2 [/latex] = selisih frekuensi kelas modus dengan kelas sesudahnya.

Contoh

Tentukan modus dari data di bawah ini.

[table id=35 /]

Penyelesaian

Karena frekuensi terbanyak ada pada kelas 71 – 80, maka kelas modus ada pada interval kelas 71 – 80.

Dari tabel diketahui bahwa

[latex] B_{mod} [/latex] = 70,5

[latex] c [/latex] = 10

[latex] b_1 [/latex] = 24 – 14 = 10

[latex] b_2 [/latex] = 24 – 20 = 4

[latex] Mo = B_{mod} + c (\frac{b_1}{b_1+b_2})[/latex] [latex] Mo = 70,5 + 10 (\frac{10}{10+4})[/latex] [latex] Mo = 70,5 + 10 (\frac{10}{14})[/latex] [latex] Mo = 77,64[/latex]

Median (Nilai Tengah)

Median (Me) adalah nilai tengah suatu data jika data tersebut telah diurutkan dari nilai data terkecil hingga terbesar.

Median data tunggal

Untuk menentukan median data tunggal dapat ditentukan dengan cara sebagai berikut.

1. Urutkan data mulai dari data terkecil.

2. Median ditentukan dengan rumus sebagai berikut.

Untuk n ganjil

[latex] Me = X \frac{n+1}{2} [/latex]

Untuk n genap

[latex] Me = \frac{1}{2} (X \frac{n}{2} + X_{\frac{n}{2}+1}) [/latex]

Keterangan

[latex]X \frac{n}{2}[/latex] adalah data pada urutan ke [latex]\frac{n}{2}[/latex].

Contoh

Tentukan median dari data di bawah ini.

1. 6; 7; 8; 6; 8
2. 6; 7; 8; 6; 8; 5; 6; 9; 7; 6

Penyelesaian

1. Urutkan data dari yang terkecil
   6; 6; 7; 8; 8Karena n = 5 ganjil, maka[latex] Me = X \frac{n+1}{2} = X \frac{5+1}{2} = X \frac{6}{2} = X_3 = 7 [/latex]
2. Urutkan data dari yang terkecil
   5; 6; 6; 6; 6; 7; 7; 8; 8; 9Karena n = 10 genap, maka[latex] Me = \frac{1}{2} (X \frac{n}{2} + X_{\frac{n}{2}+1}) = \frac{1}{2} (X \frac{10}{2} + X_{\frac{10}{2}+1}) = \frac{1}{2} (X_5 + X_6) = \frac{6+7}{2} = 6,5 [/latex]

Median data berkelompok

Untuk menentukan median data berkelompok dapat digunakan rumus sebagai berikut.

[latex] Me = B_med + c (\frac {\frac{1}{2}n-F}{f}) [/latex]

Keterangan

Me = median

[latex] B_{med} [/latex] = batas bawah kelas median (kelas yang memuat median)

c = panjang interval kelas median

n = banyaknya data

F = frekuensi kumulatif sebelum kelas median

f = frekuensi kelas median

Contoh

Diketahui skor UAS matematika di bawah ini

[table id=36 /]

Berapakah mediannya?

Penyelesaian

Karena , maka mediannya terletak di antara [latex] X_40 [/latex] dan [latex] X_41 [/latex], sehingga kelas median pada interval 71 – 80.

Dari tabel di atas diketahui bahwa

[latex] B_{med} [/latex] = 70,5

c = 10

n = 80

F = 24

f = 24

[latex] Me = B_med + c (\frac {\frac{1}{2}n-F}{f}) [/latex]

 

[latex] Me = 70,5 + 10 (\frac {\frac{1}{2} \times 80 – 24}{24}) [/latex]

 

[latex] Me = 70,5 + 10 (\frac {16}{24}) [/latex]

 

[latex] Me = 70,5 + 6,7 [/latex]

 

[latex] Me = 77,2 [/latex]

Jadi, mediannya adalah 77,2.