Rumus luas segitiga adalah L = 1/2 × a × t , dengan L = Luas segitiga, a = panjang sisi alas segitiga dan t = tinggi segitiga.
Untuk menghitung seberapa luas suatu bangun datar segitiga, maka yang anda butuhkan adalah rumus luas segitiga. Pada kesempatan kali ini kita akan bahas secara lengkap cara menghitung luas segitiga. Bahkan ada rumus yang lain juga loh. Untuk lebih jelasnya simak pembahasan berikut ini.
Daftar isi
Rumus Luas Segitiga
| Nama | Rumus |
| Luas | L = ½ × a × t |
| L = √(s × (s-a)×(s-b)×(s-c)) |
Keterangan
- L = luas segitiga
- a = sisi alas segitiga
- t = tinggi segitiga
- s = ½ keliling segitiga
- b = sisi segitiga
- c = sisi segitiga
2 Cara Menghitung Luas Segitiga
1. Menggunakan alas dan tinggi segitiga
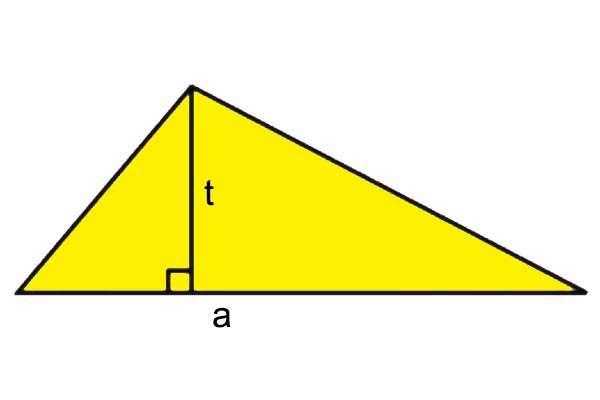
Cara pertama untuk menghitung luas segitiga adalah dengan memanfaatkan tinggi segitiga. Tinggi segitiga adalah Jarak antara salah satu titik segitiga dengan sisi yang ada di depannya.
Jarak tersebut didapatkan dengan cara menarik garis tegak lurus dari titik menuju ke sisi di depan titik tersebut. Panjang garis itulah yang kita sebut sebagai tinggi segitiga. Sehingga rumus luas segitiga adalah
L = ½×a×t
Keterangan
- L = Luas Segitiga
- a = alas segitiga atau sisi yang dihubungkan dengan titik untuk mencari tinggi.
- t = tinggi segitiga
Rumus ini dapat digunakan untuk semua jenis segitiga. Baik itu segitiga sembarang, siku-siku, sama kaki, maupun sama sisi.
Segitiga siku-siku memiliki sudut siku-siku pada salah satu sudutnya. Sehingga salah satu sisi segitiga tersebut dapat digunakan sebagai tinggi segitiga.
Contoh Soal
1. Diketahui suatu segitiga siku-siku memiliki alas dengan panjang 12 cm dan tinggi 5 cm. Hitunglah luas segitiga tersebut!
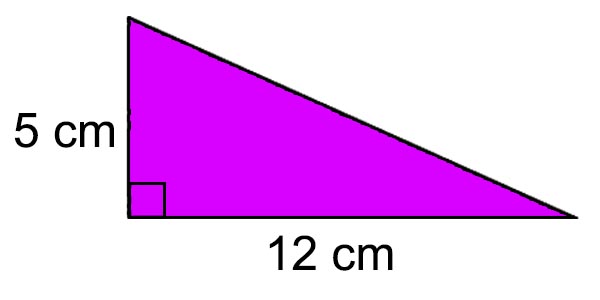
Jawaban :
Diketahui a = 12 cm dan t = 5 cm
L = ½×a×t
L = ½×12×5
L = 30 cm²
Jadi, luas segitiga tersebut adalah 30 cm².
2. Hitunglah luas segitiga berikut ini!
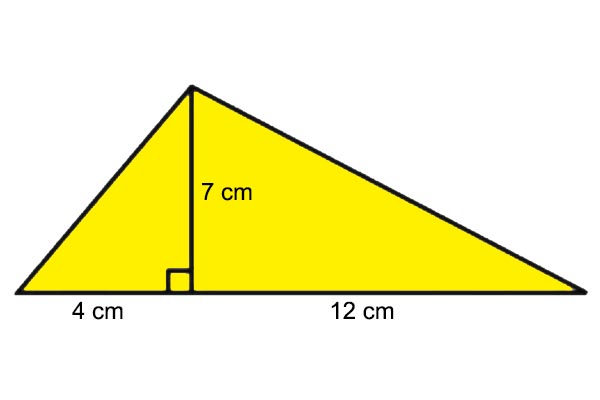
Jawaban :
Diketahui t = 7 cm dan a = 4 + 12 = 16 cm
L = ½×a×t
L = ½×16×7
L = 8×7
L = 56 cm²
Jadi, luas segitiga tersebut adalah 56 cm².
2. Menggunakan Keliling Segitiga
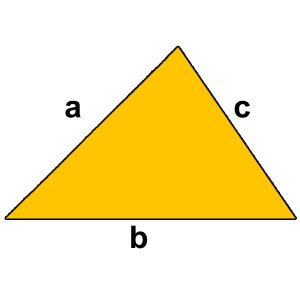
Rumus ini mungkin dapat anda gunakan sebagai alternatif. Ketika anda kesulitan dalam mencari tinggi segitiga. Anda bisa memanfaatkan keliling segitiga untuk menghitung luas. Rumusnya adalah
L = √(s×(s-a)×(s-b)×(s-c))
Keterangan
- L = Luas Segitiga
- s = ½ keliling segitiga
- a, b dan c = sisi-sisi segitiga
Biasanya rumus ini digunakan ketika mencari luas segitiga sembarang. Atau untuk jenis segitiga lainnya ketika sudah malas mencari tinggi segitiga.
Sehingga rumus ini dapat digunakan untuk semua jenis segitiga dengan syarat diketahui semua panjang sisinya. Untuk lebih jelasnya, perhatikan contoh berikut ini.
Contoh Soal
Hitunglah luas segitiga yang memiliki panjang sisi 6 cm, 8 cm dan 12 cm!
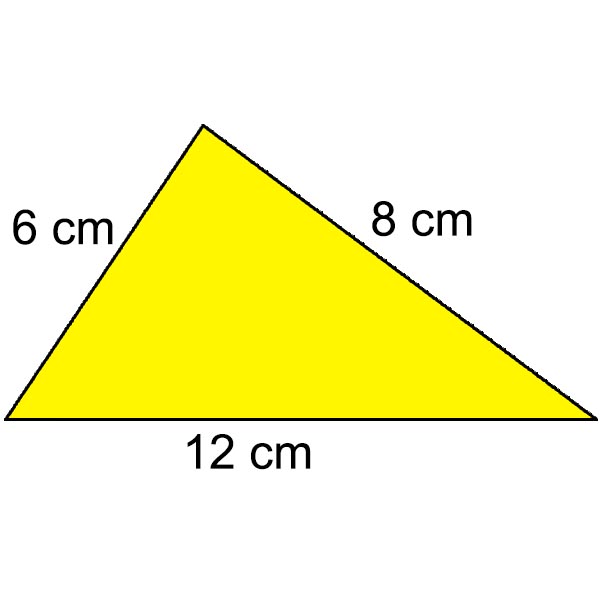
Jawaban:
Diketahui a = 6 cm, b = 8 cm , dan c = 12 cm
K = 6 + 8 + 12
K = 26 cm
s = ½K
s = 13 cm
Ditanyakan
L = ?
L = √(s×(s-a)×(s-b)×(s-c))
L = √(13×(13-6)×(13-8)×(13-12))
L = √(13×7×5×1)
L = √455 cm²
Jadi, luas segitiga tersebut adalah √455 cm².
2. Hitunglah luas segitiga siku-siku berikut ini!
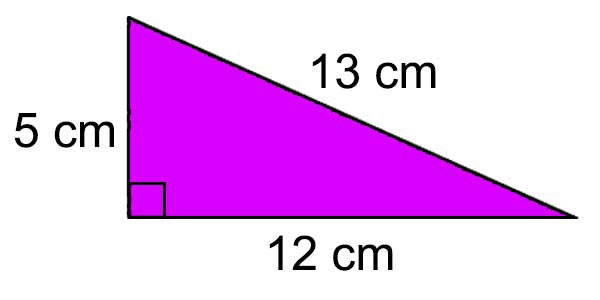
Jawaban :
Diketahui a = 5 cm, b = 12 cm, dan c = 13 cm
K = 5+12+13
K = 30 cm
s = ½K
s = 15 cm
Ditanyakan
L = ?
L = √(s×(s-a)×(s-b)×(s-c))
L = √(15×(15-5)×(15-12)×(15-13))
L = √(15×10×3×2)
L = √(150 × 6)
L = √900
L = 30 cm²
Jadi, luas segitiga tersebut adalah 30 cm².
Kesimpulan
Dengan ini kita dapat simpulkan bahwa untuk mencari luas segitiga ada 2 metode yang dapat digunakan. Yaitu menggunakan alas dan tinggi segitiga atau menggunakan keliling segitiga.
Mungkin cukup sekian yang dapat kami sampaikan. Semoga bermanfaat untuk kita semua. Jangan lupa untuk share dengan teman-teman lainnya untuk menambah wawasan.

Seorang mahasiswa pendidikan matematika di Universitas Muhammadiyah Purwokerto yang suka bermain dengan logika. Founder teknikece.com