Rumus Volume Tabung

Rumus volume tabung adalah V = π × r × r × t , dengan V = Volume tabung; π = 22/7 atau 3,14 ; r = jari-jari alas tabung dan t = tinggi tabung.

---

Untuk mengetahui volume atau kapasitas suatu bangun ruang tabung, maka yang kita butuhkan adalah rumus volume tabung.

Pada dasarnya, untuk menghitung volume tabung itu gampang banget temen-temen. Karena tabung termasuk dalam kategori bangun ruang prisma.

Yaitu bangun ruang yang memiliki bentuk alas dan tutup yang kongruen (sama besar). Sehingga untuk menghitung volumenya kalian cukup kalikan luas alas tabung dengan tinggi tinggi tabung. Untuk lebih jelasnya simak pembahasan berikut ini.

Rumus Volume Tabung

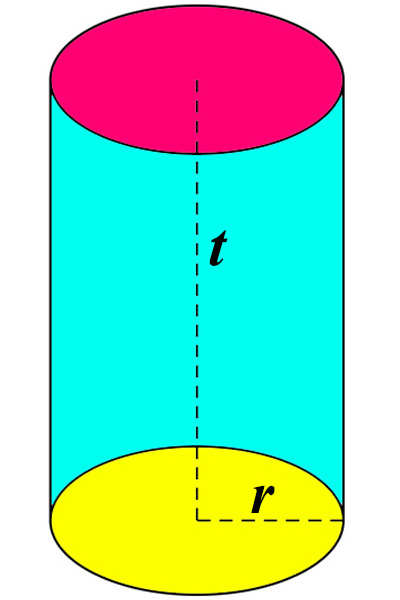
V = π×r²×t

Keterangan

• V = Volume tabung
• π = 22/7 atau 3,14
• r = jari-jari alas tabung
• t = tinggi tabung

Cara Menghitung Volume Tabung

Rumus volume tabung didapatkan dari kombinasi rumus prisma dan luas lingkaran. Karena kita tahu bahwa tabung adalah bangun ruang prisma yang memiliki alas berbentuk lingkaran.

Sehingga rumus volume tabung adalah

V = π×r²×t

Untuk lebih jelasnya, kamu bisa lihat contoh soal berikut ini.

Contoh Soal Volume Tabung

1. Suatu tabung memiliki jari-jari sepanjang 14 cm dan tinggi 25 cm. Hitunglah volume tabung tersebut!

Jawaban :

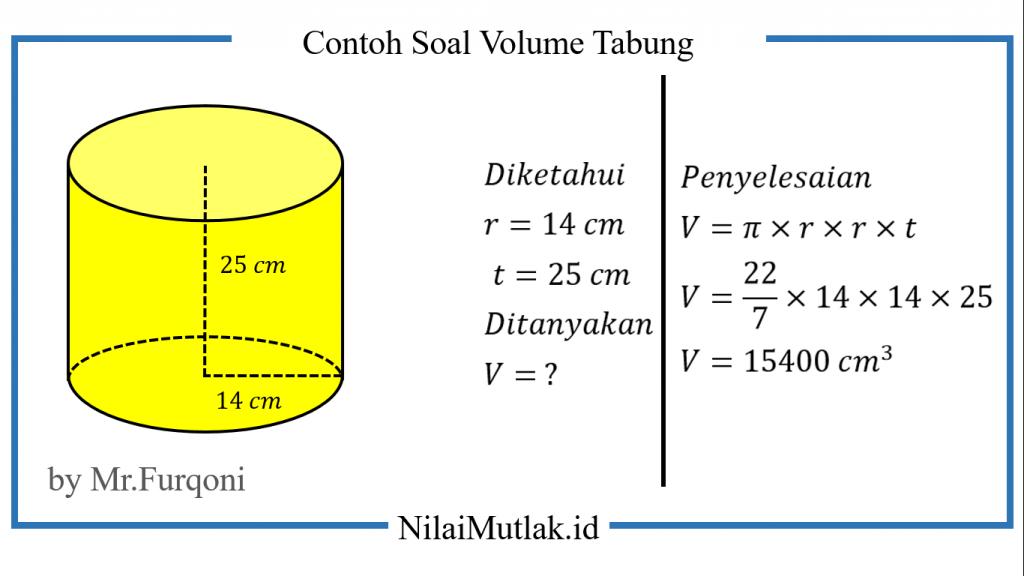
Jadi, volume tabung tersebut adalah 15400 cm³.

2. Hitunglah volume tabung yang memiliki jari-jari sepanjang 10 cm dan tinggi 28 cm!

Jawaban :

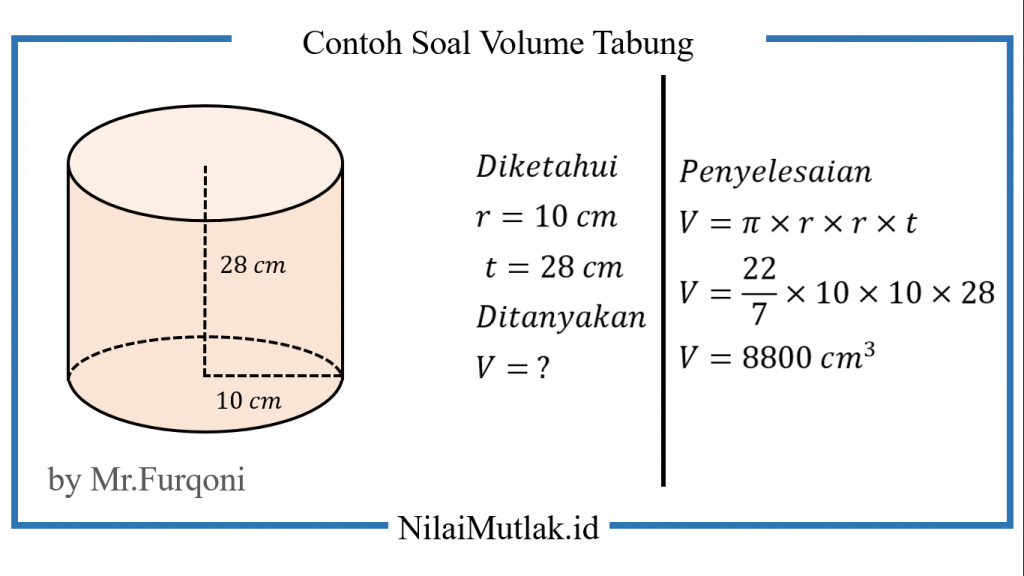
Jadi, volume tabung tersebut adalah 8800 cm³.

3. Jika suatu tabung memiliki jari-jari 8 cm dan tinggi 15 cm, berapakah volumenya?

Jawaban :

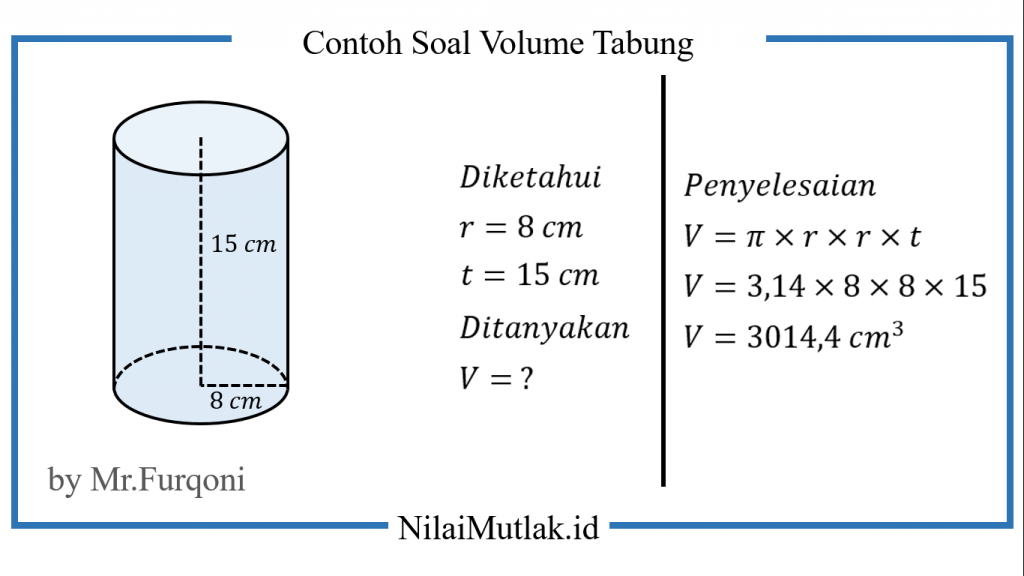
Jadi, volume tabung tersebut adalah 3014,4 cm³.

Bagaimana temen-temen? Ternyata gampang banget kan untuk menghitung volume tabung.

Kalian cukup kalikan luas alasnya yang berupa lingkaran dengan tinggi tabungnya. Demikianlah pembahasan lengkap mengenai rumus volume tabung beserta dengan contoh soalnya.

Semoga bermanfaat dan menambah wawasan kita semua. Jangan lupa untuk share informasi ini dengan teman-teman yang lainnya.