Sin cos tan adalah istilah yang ada dalam trigonometri. Ilmu ini sangat penting untuk dikuasai. Apalagi untuk anda yang sedang menempuh jenjang SMA atau SMK. 

Karena ada banyak sekali soal-soal Ujian Nasional, Ujian Sekolah bahkan Ujian Masuk Perguruan Tinggi yang berkaitan dengan trigonometri. Tak hanya itu saja. Dalam perancangan suatu konstruksi, trigonometri juga sangat berguna.

Maka dari itu kali ini kita akan bahas lebih dalam lagi mengenai trigonometri. Agar anda benar-benar siap mengunakan rumus-rumus trigonometri.

Pengertian Trigonometri

Trigonometri berasal dari bahasa Yunani yaitu dari kata “trigonon” yang berarti tiga sudut, dan “metron” yang berarti mengukur.adalah cabang ilmu dari matematika yang mempelajari tentang hubungan antara panjang sisi dan sudut dalam segitiga siku-siku. 

Karena sejatinya trigonometri adalah perbandingan antara sisi tegak, sisi miring, dan sisi samping (alas) dalam segitiga siku-siku.

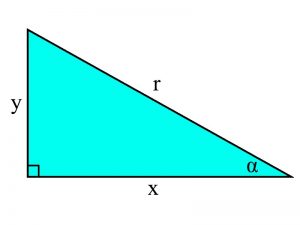
Perhatikan segitiga siku-siku berikut ini untuk memudahkan anda dalam memahami trigonometri.

Sin

Sin atau Sinus adalah perbandingan antara sisi tegak dan sisi miring dari suatu sudut. Contohnya

Sin ⍺ = y/r

Cos

Cos atau Cosinus adalah perbandingan antara sisi samping dengan sisi miring. Contohnya

Cos ⍺ = x/r

Tan

Tan atau Tangen adalah perbandingan antara sisi tegak dan sisi samping atau perbandingan antara nilai sin dan cos sudut yang sama. Contohnya

Tan ⍺ = Sin ⍺/Cos ⍺ = y/x

Cosec

Cosec atau Cosecan adalah perbandingan antara sisi miring dengan sisi tegak atau kebalikan dari sin. Contoh

Cosec ⍺ = 1/sin ⍺ = r/y

Sec

Sec atau Secan adalah perbandingan antara sisi miring dengan sisi samping atau kebalikan dari cos. Contoh

Sec ⍺ = 1/cos ⍺ = r/x

Cotan

Cotan atau Cotangen adalah perbandingan antara sisi samping dengan sisi tegak atau kebalikan dari tan. Contoh

Cot ⍺ = 1/Tan ⍺ = x/y

Contoh Soal

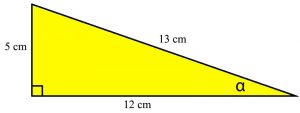
Carilah nilai sin ⍺, cos ⍺, tan ⍺, sec ⍺, cosec ⍺, dan cot ⍺ dari segitiga tersebut!

Sin ⍺ = 5/13 cm

Cos ⍺ = 12/13 cm

Tan ⍺ = 5/12 cm

Cosec ⍺ = 13/5 cm

Sec = 13/12 cm

Cot = 12/5 cm

Identitas Trigonometri

Sin² α + Cos² α = 1

Sin² A  = 1 – Cos² A 

Cos² A = 1 – Sin² A 

1 + Tan² α = 1 ÷ Cos² α = Sec² α

1 + Cot² α = 1 ÷ Sin² α = Cosec² α

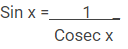
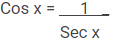
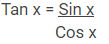
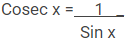
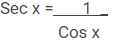
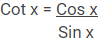
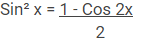
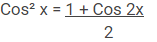
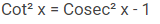
Penjumlahan dan Selisih Trigonometri

Sin (α + β) = Sin α Cos β + Cos α Sin β

Sin (α – β) = Sin α Cos β – Cos α Sin β

Cos (α + β) = Cos α Cos β – Sin α Sin β

Cos (α – β) = Cos α Cos β + Sin α Sin β

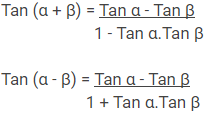
Rumus Trigonometri sudut Rangkap

Yaitu apabila sudut yang dijumlahkan memiliki besar yang sama. Atau α = β

Pertama

Sin (α + β) = Sin α Cos β + Cos α Sin β

Subtitusikan nilai α = β

Sin (α + α) = Sin α Cos α + Cos α Sin α

Sin 2α = 2 Sin α Cos α

Kedua

Cos (α + β) = Cos α Cos β – Sin α Sin β

Subtitusikan nilai α = β

Cos (α + α) = Cos α Cos α – Sin α Sin α

Cos 2α = Cos² α – Sin² α

Karena hasilnya merupakan selisih kuadrat, maka kita dapat memasukkan identitas trigonometri. Yaitu Sin² α + Cos² α = 1 → Sin² α = 1 – Cos² α.

Cos 2α = Cos² α – (1 – Cos² α)

Cos 2α = Cos² α – 1 + Cos² α

Cos 2α = 2 Cos² α – 1

Ketiga

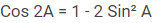
Keempat

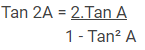
Rumus Trigonometri Sudut Tengahan

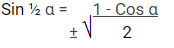
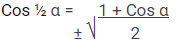
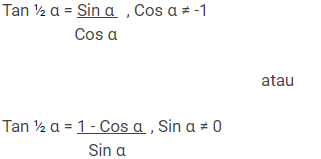
Perkalian Trigonometri

Rumus Pertama

Jumlahkan antara Sin (α + β) dengan Sin (α – β). Maka diperoleh

Sin (α + β) + Sin (α – β) = Sin α Cos β + Cos α Sin β + Sin α Cos β – Cos α Sin β

Sin (α + β) + Sin (α – β) = 2 Sin α Cos β

Sehingga didapatkan rumus

Sin α Cos β = ½ × (Sin (α + β) + Sin (α – β))

Rumus Kedua

Hitung selisih dari Sin (α + β) dengan Sin (α – β). Maka diperoleh

Sin (α + β) – Sin (α – β) = Sin α Cos β + Cos α Sin β – Sin α Cos β + Cos α Sin β

Sin (α + β) – Sin (α – β) = 2 Cos α Sin β

Sehingga didapatkan rumus

Cos α Sin β = ½ × (Sin (α + β) – Sin (α – β))

Rumus Ketiga

Jumlahkan antara Cos (α + β) dengan Cos (α – β). Maka diperoleh

Cos (α + β) + Cos (α – β) = Cos α Cos β – Sin α Sin β + Cos α Cos β + Sin α Sin β

Cos (α + β) + Cos (α – β) = 2 Cos α Cos β

Sehingga didapatkan rumus

Cos α Cos β = ½ × (Cos (α + β) + Cos (α – β))

Rumus Keempat

Hitung selisih dari Cos (α + β) dengan Cos (α – β). Maka diperoleh

Cos (α + β) – Cos (α – β) = Cos α Cos β – Sin α Sin β – Cos α Cos β – Sin α Sin β

Cos (α + β) – Cos (α – β) = – 2 Sin α Sin β

Sehingga didapatkan rumus

Sin α Sin β = – ½ × (Cos (α + β) – Cos (α – β))

Rumus Penjumlahan dan Pengurangan Sinus dan Cosinus

Sin α + Sin β = 2. Sin ½ (α + β) . Cos ½ (α – β)

Sin α – Sin β = 2. Cos ½ (α + β) . Sin ½ (α – β)

Cos  α + Cos β = 2. Cos ½ (α + β) . Cos ½ (α – β) 

Cos  α – Cos β = – 2. Sin ½ (α + β) . Sin ½ (α – β)

Rumus Perkalian Sinus dan Cosinus

Rumus Pertama

Rumus Kedua

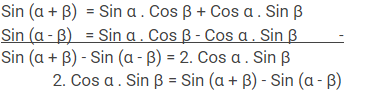
Rumus Ketiga

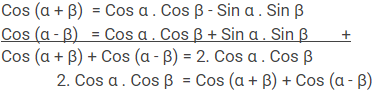
Rumus Keempat

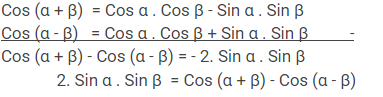
Rumus Limit Trigonometri

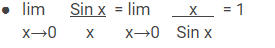
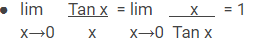
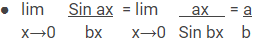
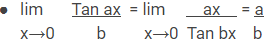
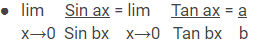
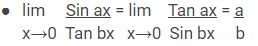
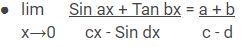
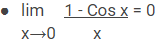
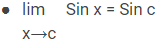
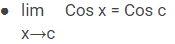
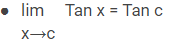
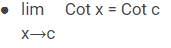
Rumus Turunan Trigonometri

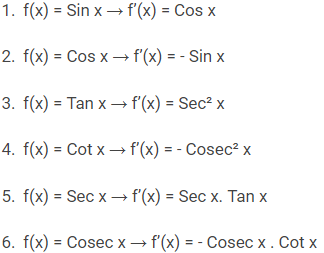
Rumus Integral Trigonometri

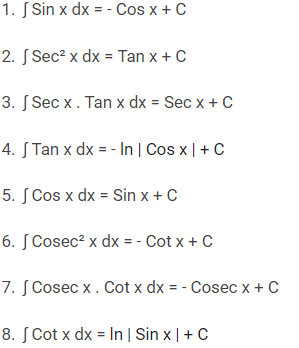
Tabel Sin Cos Tan atau Tabel Trigonometri

Tabel sin cos tan adalah tabel yang berisi nilai trigonometri mulai dari 0° sampai 360°. Karena  kita mengetahui bahwa suatu lingkaran penuh memiliki sudut 360°.

Tabel trigonometri ini sangat berguna dalam perhitungan sudut. Sehingga anda harus mengetahui nilai trigonometri untuk sudut istimewa atau pun sudut lainnya.

Nilai sin cos tan setiap sudut berbeda-beda. Untuk memudahkan anda dalam mengetahui nilai sin cos tan suatu sudut kami telah menyediakan tabel yang berisi nilai trigonometri untuk semua sudut.

Tabel Sin Cos Tan Sudut Istimewa

Tabel Trigonometri Sudut Istimewa Kuadran 1 (Sudut 0° – 90°)

[table id=25 /]

Tabel Trigonometri Sudut Istimewa Kuadran 2 (Sudut 90° – 180°)

[table id=26 /]

Tabel Trigonometri Sudut Istimewa Kuadran 3 (Sudut 180° – 270°)

[table id=27 /]

Tabel Trigonometri Sudut Istimewa Kuadran 4 (Sudut 270° – 360°)

[table id=28 /]

Tabel Trigonometri Sudut Istimewa Satu Lingkaran Penuh (Sudut 0° – 360°)

[table id=29 /]

Tabel Sin Cos Tan Seluruh Sudut

Tabel Trigonometri Kuadran 1 (Sudut 0° – 90°)

[table id=19 /]

Tabel Trigonometri Kuadran 2 (Sudut 90° – 180°)

[table id=21 /]

Tabel Trigonometri Kuadran 3 (Sudut 180° – 270°)

[table id=22 /]

Tabel Trigonometri Kuadran 4 (Sudut 270° – 360°)

[table id=23 /]